2 Datos geográficos en R

Prerrequisitos

Este es el primer capítulo práctico del libro y, por lo tanto, conlleva algunos requisitos de software. Suponemos que ya tienes instalada una versión actualizada de R y que te sientes cómodo utilizando el software con una interfaz de línea de comandos como el entorno de desarrollo integrado (IDE) RStudio.

Si eres nuevo en R, te recomendamos leer el capítulo 2 del libro en línea Efficient R Programming de Gillespie and Lovelace (2016) y aprender los fundamentos del lenguaje con recursos como R for Data Science de Grolemund and Wickham (2016). Organiza tu trabajo (por ejemplo, con proyectos de RStudio) y asigna a los scripts nombres sensatos como 02-chapter.R para documentar el código que escribes a medida que aprendes.

Los paquetes utilizados en este capítulo pueden instalarse con los siguientes comandos:⁴

install.packages("sf")
install.packages("terra")
install.packages("spData")
install.packages("spDataLarge", repos = "https://nowosad.r-universe.dev")

Si estás trabajando con Mac o Linux, es posible que el comando anterior para instalar sf no funcione la primera vez. Estos sistemas operativos (SO) tienen “requisitos del sistema” que se describen en el README del paquete. Se pueden encontrar varias instrucciones específicas para cada SO en línea, como el artículo Instalación de R 4.0 en Ubuntu 20.04 (Installation of R 4.0 on Ubuntu 20.04 en inglés) en el blog rtask.thinkr.fr.

Todos los paquetes necesarios para reproducir el contenido del libro se pueden instalar con el siguiente comando: remotes::install_github("geocompr/geocompkg"). Los paquetes necesarios se pueden “cargar” (técnicamente se adjuntan) con la función library() de la siguiente manera:

library(sf)          # clases y funciones para datos vectoriales
#> Linking to GEOS 3.10.2, GDAL 3.4.1, PROJ 8.2.1; sf_use_s2() is TRUE

La salida de library(sf) informa de las versiones de las bibliotecas geográficas clave (key geographic libraries), como GEOS, la cual ya está utilizando el paquete, como se indica en la Sección 2.2.1.

library(terra)      # clases y funciones para datos rasterizados

Los demás paquetes instalados contienen datos que se utilizarán en el libro:

library(spData)        # cargar datos geográficos
library(spDataLarge)   # cargar datos geográficos de mayor tamaño

2.1 Introducción

En este capítulo se explicarán brevemente los modelos de datos geográficos fundamentales: vectorial y rasterizado. Introduciremos la teoría detrás de cada modelo de datos y las disciplinas en las que predominan, antes de demostrar su implementación en R.

El modelo de datos vectoriales representa el mundo mediante puntos, líneas y polígonos. Estos tienen bordes discretos y bien definidos, lo que significa que los conjuntos de datos vectoriales suelen tener un alto nivel de precisión (pero no necesariamente exactitud, como veremos en el apartado 2.5). El modelo de datos ráster divide la superficie en celdas de tamaño constante. Los conjuntos de datos ráster son la base de las imágenes de fondo utilizadas en la cartografía web y han sido una fuente vital de datos geográficos desde los orígenes de la fotografía aérea y los dispositivos de teledetección por satélite. Los rásteres agregan características espacialmente específicas a una resolución determinada, lo que significa que son consistentes en el espacio y escalables (existen muchos conjuntos de datos ráster a nivel mundial).

¿Cuál utilizar? La respuesta depende probablemente de su ámbito de aplicación:

• Los datos vectoriales tienden a dominar las ciencias sociales porque los asentamientos humanos tienden a tener fronteras discretas
• Los datos rasterizados predominan en las ciencias medioambientales debido a la dependencia de los datos de teledetección

En algunos campos hay mucho solapamiento y los conjuntos de datos ráster y vectoriales pueden utilizarse conjuntamente: los ecologistas y los demógrafos, por ejemplo, suelen utilizar tanto datos vectoriales como rasterizados. Además, es posible la conversión entre ambas formas (véase el capítulo ??). Independientemente de si tu trabajo implica un mayor uso de los conjuntos de datos vectoriales o rasterizados, merece la pena comprender el modelo de datos subyacente antes de utilizarlos, como se explica en los capítulos siguientes. Este libro utiliza los paquetes sf y raster para trabajar con datos vectoriales y conjuntos de datos raster, respectivamente.

2.2 Datos vectoriales

Ten cuidado al utilizar la palabra ‘vector’, ya que puede tener dos significados en este libro: datos vectoriales geográficos y la clase vector (nótese el tipo de letra monospace) en R. El primero es un modelo de datos, el segundo es una clase de R al igual que data.frame y matrix. Sin embargo, existe un vínculo entre ambos: las coordenadas espaciales que constituyen el núcleo del modelo de datos vectoriales geográficos pueden representarse en R mediante objetos vectoriales.

El modelo de datos vectoriales geográficos se basa en puntos situados dentro de un sistema de referencia de coordenadas (SRC, CRS en inglés). Los puntos pueden representar características autónomas (por ejemplo, la ubicación de una parada de autobús) o pueden estar vinculados entre sí para formar geometrías más complejas, como líneas y polígonos. La mayoría de las geometrías de puntos contienen sólo dos dimensiones (los SRC tridimensionales contienen un valor \(z\) adicional, que suele representar la altura sobre el nivel del mar).

En este sistema, Londres, por ejemplo, puede representarse con las coordenadas c(-0.1, 51.5). Esto significa que su ubicación es -0,1 grados al este y 51,5 grados al norte del origen. En este caso, el origen se encuentra a 0 grados de longitud (el Primer Meridiano o Meridiano de Greenwich) y 0 grados de latitud (Ecuador) en un SRC geográfico (‘lon/lat’) (Figura 2.1, panel izquierdo). El mismo punto también podría aproximarse en un SRC proyectado con valores ‘Este/Norte’ de c(530000, 180000) en la British National Grid, lo que significa que Londres se encuentra a 530 km al Este y 180 km al Norte del \(origen\) del SRC. Esto puede comprobarse visualmente: algo más de 5 ‘casillas’ -áreas cuadradas delimitadas por las líneas grises de la cuadrícula de 100 km de ancho- separan el punto que representa a Londres del origen (Figura 2.1, panel derecho).

La ubicación del origen de National Grid, en el mar más allá del Suroeste de la península, garantiza que la mayoría de las ubicaciones en el Reino Unido tengan valores positivos de Orientación y Longitud.⁵ Hay más aspectos sobre los SRC, como se describe en las secciones 2.4 y ??, pero, para los propósitos de esta sección, es suficiente saber que las coordenadas consisten en dos números que representan la distancia desde un origen, generalmente en \(x\) y luego \(y\) para las dimensiones.

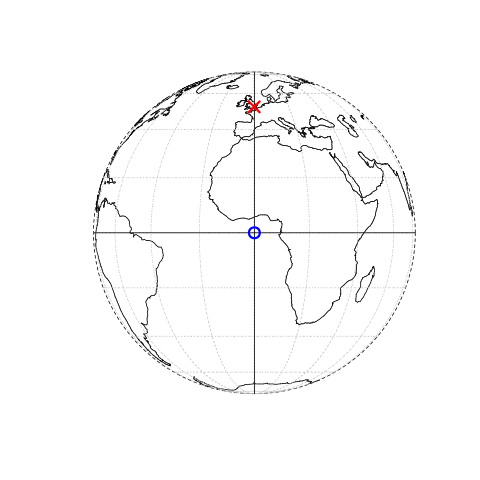
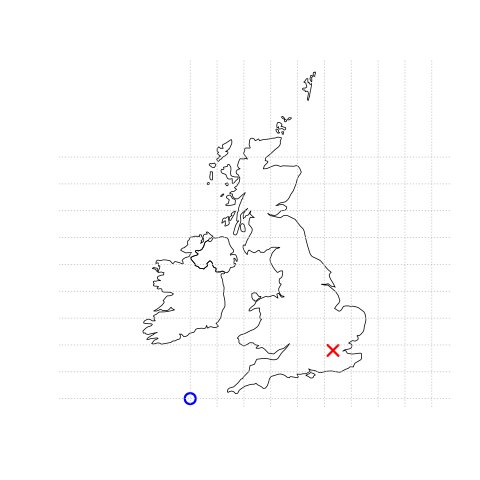
FIGURE 2.1: Ilustración de datos vectoriales (puntos) en los que la ubicación de Londres (la X roja) se representa con referencia a un origen (el círculo azul). El gráfico de la izquierda representa un SRC geográfico con un origen a 0° tanto para la longitud como para la latitud. El gráfico de la derecha representa un SRC proyectado con el origen situado en el mar al Suroeste peninsular.

sf es un paquete que proporciona un sistema de clases para datos vectoriales geográficos. sf no sólo sustituye a sp, sino que también proporciona una interfaz de línea de comandos consistente para GEOS y GDAL, sustituyendo a rgeos y rgdal (descritos en la Sección ??). Esta sección presenta las clases sf como preparación para los capítulos siguientes (los capítulos ?? y ?? cubren la interfaz de GEOS y GDAL, respectivamente).

2.2.1 Introducción a Simple Features

Simple Features (en ocasiones también llamado Simple feature access (SFA)) es un estándar abierto desarrollado y respaldado por el Open Geospatial Consortium (OGC), una organización sin ánimo de lucro cuyas actividades volveremos a tratar en un capítulo posterior (en la sección ??). Simple Features es un modelo de datos jerárquico que representa una amplia gama de tipos de geometría. De los 17 tipos de geometría que soporta la especificación, solo 7 se utilizan en la gran mayoría de las investigaciones geográficas (véase la figura 2.2); estos tipos de geometría básicos son totalmente compatibles con el paquete de R sf (Pebesma 2018).⁶

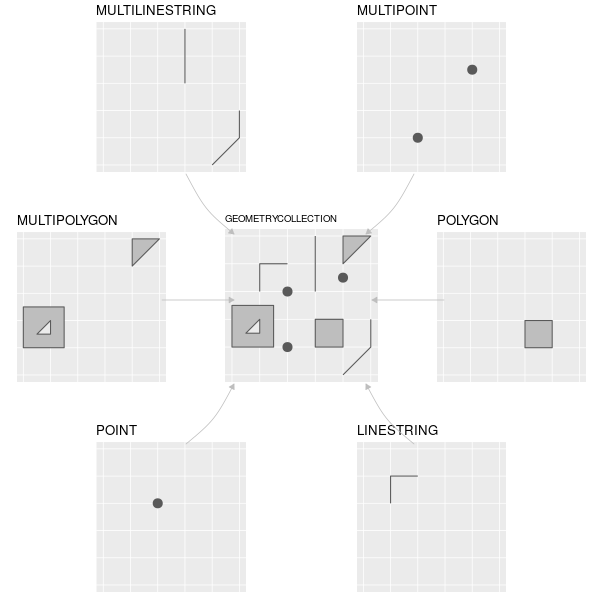
FIGURE 2.2: Tipos de Simple Features compatibles con sf.

sf puede representar todos los tipos de geometría vectorial comunes (las clases de datos rasterizados no son soportadas por sf): puntos, líneas, polígonos y sus respectivas versiones ‘multi’ (que agrupan elementos del mismo tipo en una sola función). sf también soporta colecciones geométricas, las cuales pueden contener múltiples tipos de geometrías en un solo objeto. sf proporciona la misma funcionalidad (y más) que previamente se ofrecía en tres paquetes: sp para las clases de datos (Pebesma and Bivand 2018), rgdal para la lectura/escritura de datos a través de una interfaz para GDAL y PROJ (Bivand, Keitt, and Rowlingson 2018) y rgeos para las operaciones espaciales a través de una interfaz para GEOS (Bivand and Rundel 2018). Para reiterar el mensaje del capítulo 1, los paquetes geográficos de R tienen una larga historia de interfaces con librerías de bajo nivel, y sf mantiene esta tradición con una interfaz unificada con versiones recientes de la librería GEOS para operaciones geométricas, la librería GDAL para leer y escribir archivos de datos geográficos, y la librería PROJ para representar y transformar sistemas de referencia de coordenadas proyectadas. Este es un logro notable que reduce el espacio necesario para ‘cambiar de contexto’ entre diferentes paquetes y permite el acceso a librerías geográficas de alto rendimiento. La documentación sobre sf puede encontrarse en su sitio web y en 6 ‘viñetas’, que pueden cargarse de la siguiente manera:

vignette(package = "sf") # ver qué viñetas están disponibles
vignette("sf1")          # introducción al paquete

Como se explica en la primera viñeta, los objetos ‘Simple Feature’ en R se almacenan en un marco de datos, con los datos geográficos ocupando una columna especial, normalmente llamada ‘geom’ o ‘geometry’. Utilizaremos el conjunto de datos world proporcionado por el paquete spData, cargado al principio de este capítulo (véase nowosad.github.io/spData para ver una lista de conjuntos de datos cargados por el paquete). world es un objeto espacial que contiene columnas espaciales y atributos, cuyos nombres son devueltos por la función names() (la última columna contiene la información geográfica):

names(world)
#>  [1] "iso_a2"    "name_long" "continent" "region_un" "subregion" "type"     
#>  [7] "area_km2"  "pop"       "lifeExp"   "gdpPercap" "geom"

El contenido de la columna geom proporciona a los objetos sf sus poderes espaciales: world$geom es una ‘columna lista’ que contiene todas las coordenadas de los polígonos de cada uno de los países. El paquete sf proporciona un método plot() para visualizar los datos geográficos: el siguiente comando crea la Figura 2.3.

plot(world)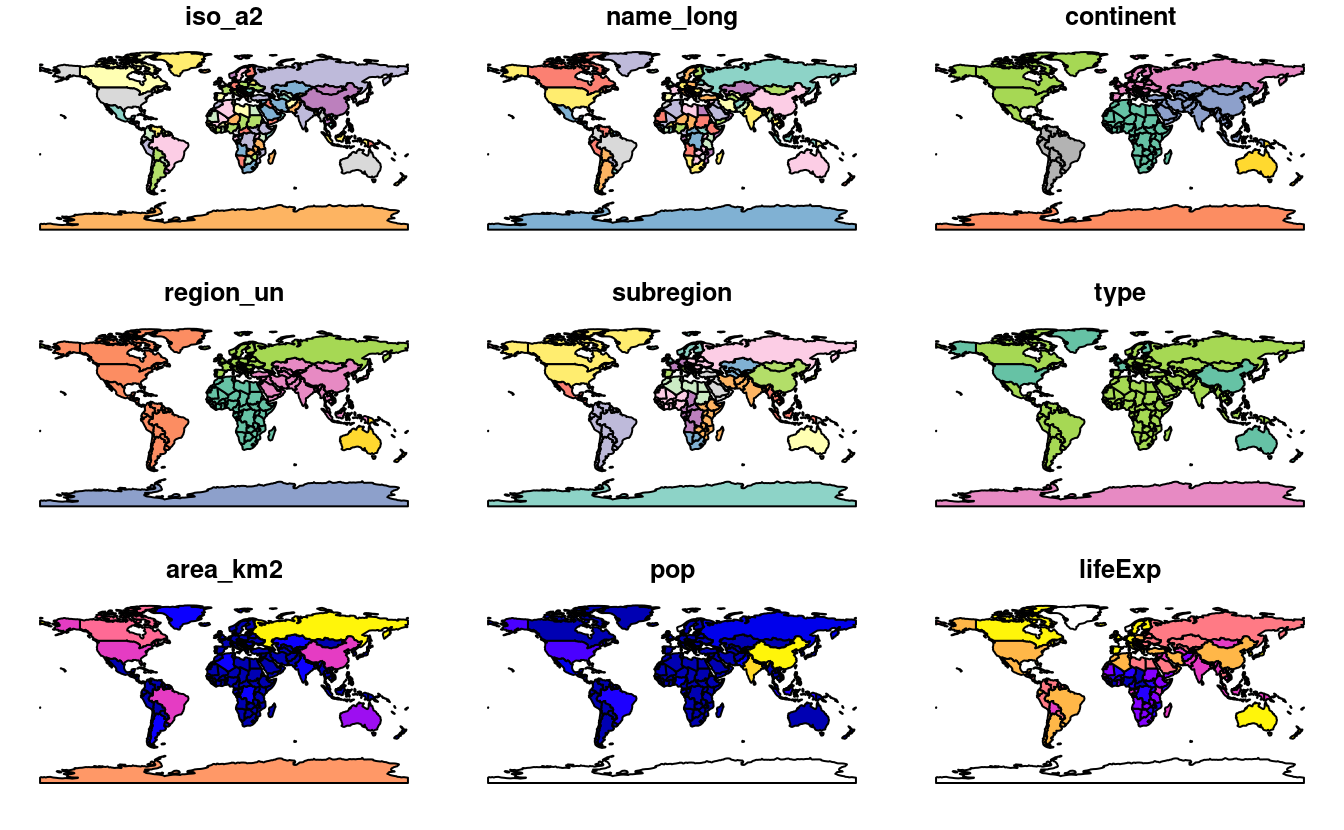

FIGURE 2.3: Un gráfico espacial del mundo utilizando el paquete sf, con un panel por cada atributo del conjunto de datos.

Observa que en lugar de crear un único mapa, como harían la mayoría de los programas SIG, el comando plot() ha creado múltiples mapas, uno para cada variable en los conjuntos de datos de world. Este procedimiento puede ser útil para explorar la distribución espacial de diferentes variables y se trata más adelante, en la sección 2.2.3.

Poder tratar los objetos espaciales como marcos de datos ordinarios pero con poderes espaciales tiene muchas ventajas, especialmente si ya estás acostumbrado a trabajar con marcos de datos. La función summary(), por ejemplo, proporciona una útil visión general de las variables dentro del objeto world.

summary(world["lifeExp"])
#>     lifeExp                geom    
#>  Min.   :50.6   MULTIPOLYGON :177  
#>  1st Qu.:65.0   epsg:4326    :  0  
#>  Median :72.9   +proj=long...:  0  
#>  Mean   :70.9                      
#>  3rd Qu.:76.8                      
#>  Max.   :83.6                      
#>  NA's   :10

Aunque sólo hemos seleccionado una variable para el comando summary, éste también emite un informe sobre la geometría. Esto demuestra el comportamiento “pegajoso” de las columnas con geometrías de los objetos sf, lo que significa que los datos geométricos se mantienen a menos que el usuario las elimine deliberadamente, como veremos en la sección @ref(Manipulación-de-atributos-vectoriales). El resultado proporciona un rápido resumen de los datos espaciales y no espaciales contenidos en world: la media de la esperanza de vida es de 71 años (oscilando entre menos de 51 y más de 83 años, con una mediana de 73 años) en todos los países.

La palabra MULTIPOLYGON (Multipolígono en español) en el resultado del sumario anterior se refiere al tipo de geometría de las figuras (países) en el objeto world. Esta representación es necesaria para países con islas como Indonesia y Grecia. Otros tipos de geometría se describen en el apartado 2.2.5.

Merece la pena profundizar en el comportamiento y el contenido básicos de este objeto Simple feature, que puede considerarse útilmente como un ‘marco de datos espaciales’ (‘Spatial data frame’ en inglés).

Los objetos sf son fáciles de subdividir. El código siguiente muestra sus dos primeras filas y tres columnas. El resultado muestra dos diferencias importantes en comparación con un data.frame normal: la inclusión de datos geográficos adicionales (tipo de geometría, dimensión, bbox e información SRC - epsg (SRID), proj4string), y la presencia de una columna de geometría, aquí denominada geom:

world_mini = world[1:2, 1:3]
world_mini
#> Simple feature collection with 2 features and 3 fields
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -180 ymin: -18.3 xmax: 180 ymax: -0.95
#> Geodetic CRS:  WGS 84
#> # A tibble: 2 × 4
#>   iso_a2 name_long continent                                                geom
#>   <chr>  <chr>     <chr>                                      <MULTIPOLYGON [°]>
#> 1 FJ     Fiji      Oceania   (((-180 -16.6, -180 -16.5, -180 -16, -180 -16.1, -…
#> 2 TZ     Tanzania  Africa    (((33.9 -0.95, 31.9 -1.03, 30.8 -1.01, 30.4 -1.13,…

Todo esto puede parecer bastante complejo, especialmente para un sistema de clases que se supone que es sencillo. Sin embargo, hay buenas razones para organizar las cosas de esta manera y utilizar sf.

Antes de describir cada tipo de geometría que permite el paquete sf, vale la pena dar un paso atrás para entender los bloques de construcción de los objetos sf. La sección 2.2.8 muestra cómo los objetos Simple features son marcos de datos, con columnas especiales de geometría. Estas columnas espaciales suelen llamarse geom o geometry: world$geom se refiere al elemento espacial del objeto world descrito previamente. Estas columnas de geometría son ‘columnas lista’ de la clase sfc (véase el apartado 2.2.7). A su vez, los objetos sfc (Simple Feature geometry list-Column) se componen de uno o varios objetos de la clase sfg (Simple Feature Geometries): geometrías simples que se describen en la sección 2.2.6.

Para entender cómo funcionan los componentes espaciales de simple features, es vital entender las geometrías simples (sfg). Por este motivo, en el apartado 2.2.5 se tratan todos los tipos de sfg actualmente admitidos, antes de pasar a describir cómo pueden representarse en R a partir de objetos sfg, los cuales constituyen las bases de los objetos sfc y, eventualmente, la totalidad de los objetos sf.

El fragmento de código anterior utiliza = para crear un nuevo objeto llamado world_mini en el comando world_mini = world[1:2, 1:3]. Esto se llama asignación. Un comando equivalente para obtener el mismo resultado es world_mini <- world[1:2, 1:3]. Aunque la ‘flecha’ es más comúnmente usada, usamos el símbolo = porque es ligeramente más rápido de escribir y más fácil de enseñar debido a la compatibilidad con otros lenguajes comúnmente usados como Python y JavaScript. Cuál usar es en gran medida una cuestión de preferencia, siempre y cuando seas consistente (paquetes como styler pueden ser usados para cambiar el estilo).

2.2.2 ¿Por qué Simple Features?

Simple features es un modelo de datos ampliamente aceptado que subyace en las estructuras de datos de muchas aplicaciones SIG, incluyendo QGIS y PostGIS. Una de las principales ventajas es que el uso del modelo de datos garantiza la transferencia de tu trabajo a otras configuraciones, por ejemplo, importar desde y exportar hacia otras bases de datos espaciales.

Una pregunta más específica desde la perspectiva de R es “¿por qué utilizar el paquete sf cuando sp ya está probado y comprobado?” Hay muchas razones (relacionadas con las ventajas del modelo Simple features):

• Lectura y escritura rápida de datos
• Mejora del rendimiento de los gráficos
• Los objetos sf pueden ser tratados como marcos de datos en la mayoría de las operaciones
• Las funciones sf pueden combinarse mediante el operador %>% y funcionan bien con la colección tidyverse de paquetes R
• Los nombres de las funciones sf son relativamente coherentes e intuitivos (todos comienzan por st_)

Debido a estas ventajas, algunos paquetes espaciales (como tmap, mapview y tidycensus) han añadido compatibilidades con sf. Sin embargo, la mayoría de los paquetes tardarán muchos años en hacer la transición y algunos nunca la harán. Afortunadamente, éstos aún pueden seguir utilizándose en un flujo de trabajo basado en objetos sf, convirtiéndolos a la clase Spatial utilizada en sp:

library(sp)
world_sp = as(world, Class = "Spatial")
# sp functions ...

Los objetos espaciales pueden volver a convertirse en sf de la misma manera o con st_as_sf():

world_sf = st_as_sf(world_sp)

2.2.3 Elaboración de un mapa básico

Los mapas básicos pueden crearse en sf con plot(). Por defecto, esto crea un gráfico compuesto de varios paneles (como spplot() de sp), un sub-gráfico para cada variable del objeto, como se ilustra en el panel de la izquierda en la Figura 2.4. Se produce una leyenda o “clave” con una paleta de colores continua si el objeto que se va a trazar tiene una sola variable (véase el panel de la derecha). Los colores también pueden establecerse con col =, aunque esto no creará una paleta continua ni una leyenda.

plot(world[3:6])
plot(world["pop"])

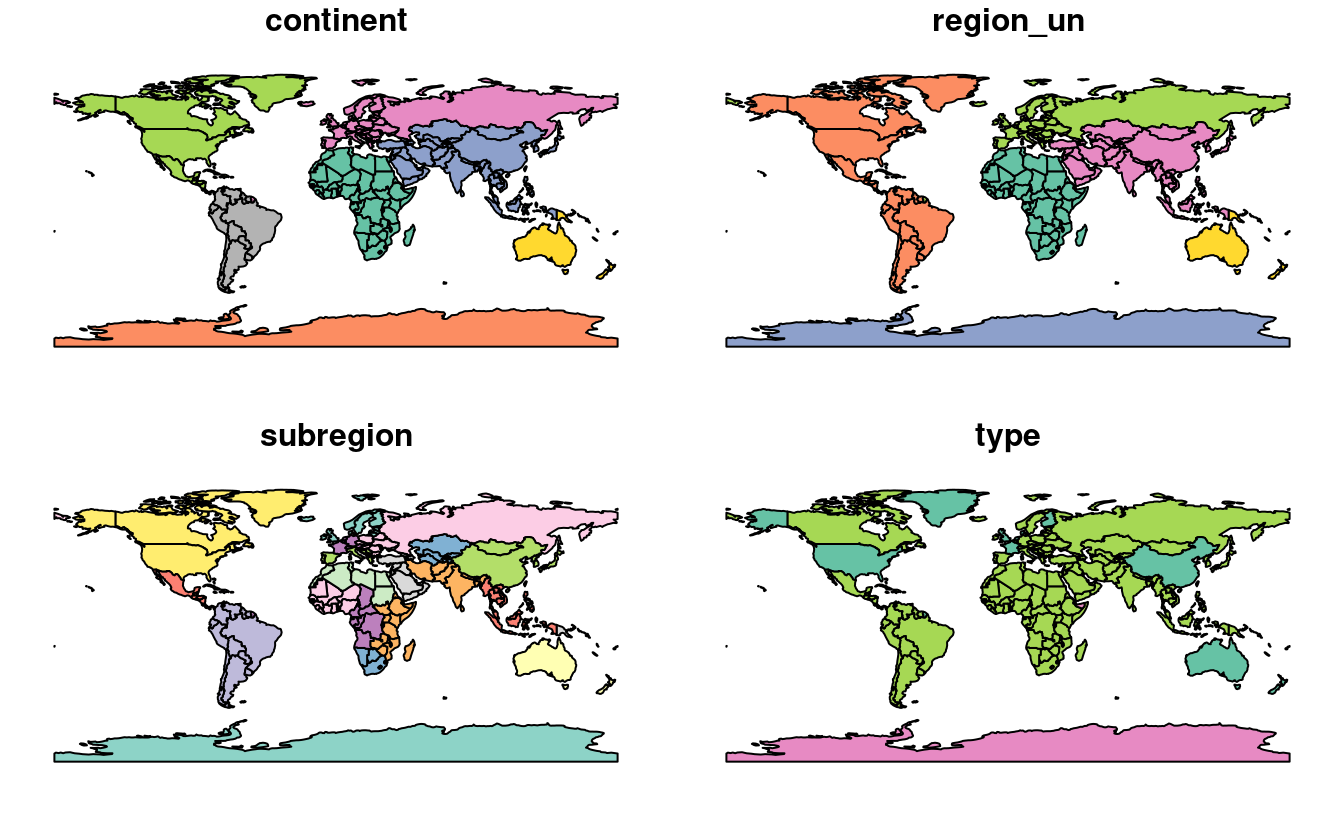
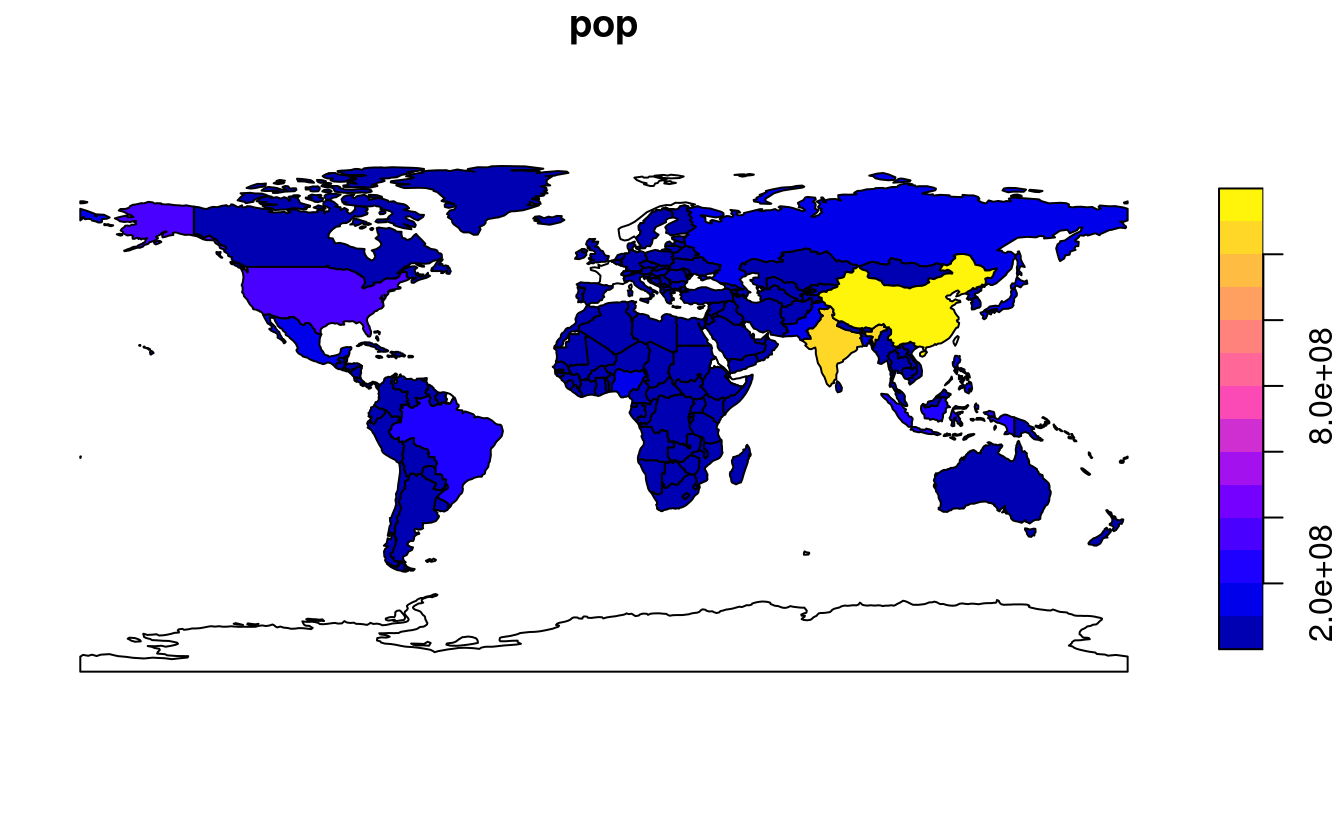
FIGURE 2.4: Gráficos con sf, con múltiples variables (izquierda) y con una única variable (derecha).

Los gráficos se añaden como capas a las imágenes existentes estableciendo add = TRUE.⁷ Para demostrar esto, y para proporcionar una muestra del contenido cubierto en los capítulos 3 y ?? sobre las operaciones de atributos y datos espaciales, el siguiente fragmento de código combina países de Asia:

world_asia = world[world$continent == "Asia", ]
asia = st_union(world_asia)

Ahora podemos representar el continente asiático sobre un mapa del mundo. Ten en cuenta que el primer gráfico sólo debe tener una variable para que add = TRUE funcione. Si el primer gráfico tiene una leyenda, debe usarse reset = FALSE (el resultado no se muestra):

plot(world["pop"], reset = FALSE)
plot(asia, add = TRUE, col = "red")

Añadir capas de esta manera puede servir para verificar la correspondencia geográfica entre capas: la función plot() es rápida de ejecutar y requiere pocas líneas de código, pero no crea mapas interactivos con una amplia gama de opciones. Para la creación de mapas más avanzados, recomendamos utilizar paquetes de visualización dedicados a ello, como tmap (véase el capítulo ??).

2.2.4 Argumentos básicos de plot()

Hay varias formas de modificar los mapas con el método plot() de sf. Dado que sf amplía los métodos de representación gráfica básicos de R, los argumentos de plot() como main = (que especifica el título del mapa) funcionan con los objetos sf (véase ?graphics::plot y ?par).⁸

La figura 2.5 ilustra esta flexibilidad superponiendo círculos, cuyos diámetros (fijados con cex =) representan las poblaciones de los países, en un mapa del mundo. Se puede crear una versión no proyectada de esta figura con los siguientes comandos (véanse los ejercicios al final de este capítulo y el script 02-contplot.R para reproducir la Figura 2.5):

plot(world["continent"], reset = FALSE)
cex = sqrt(world$pop) / 10000
world_cents = st_centroid(world, of_largest = TRUE)
plot(st_geometry(world_cents), add = TRUE, cex = cex)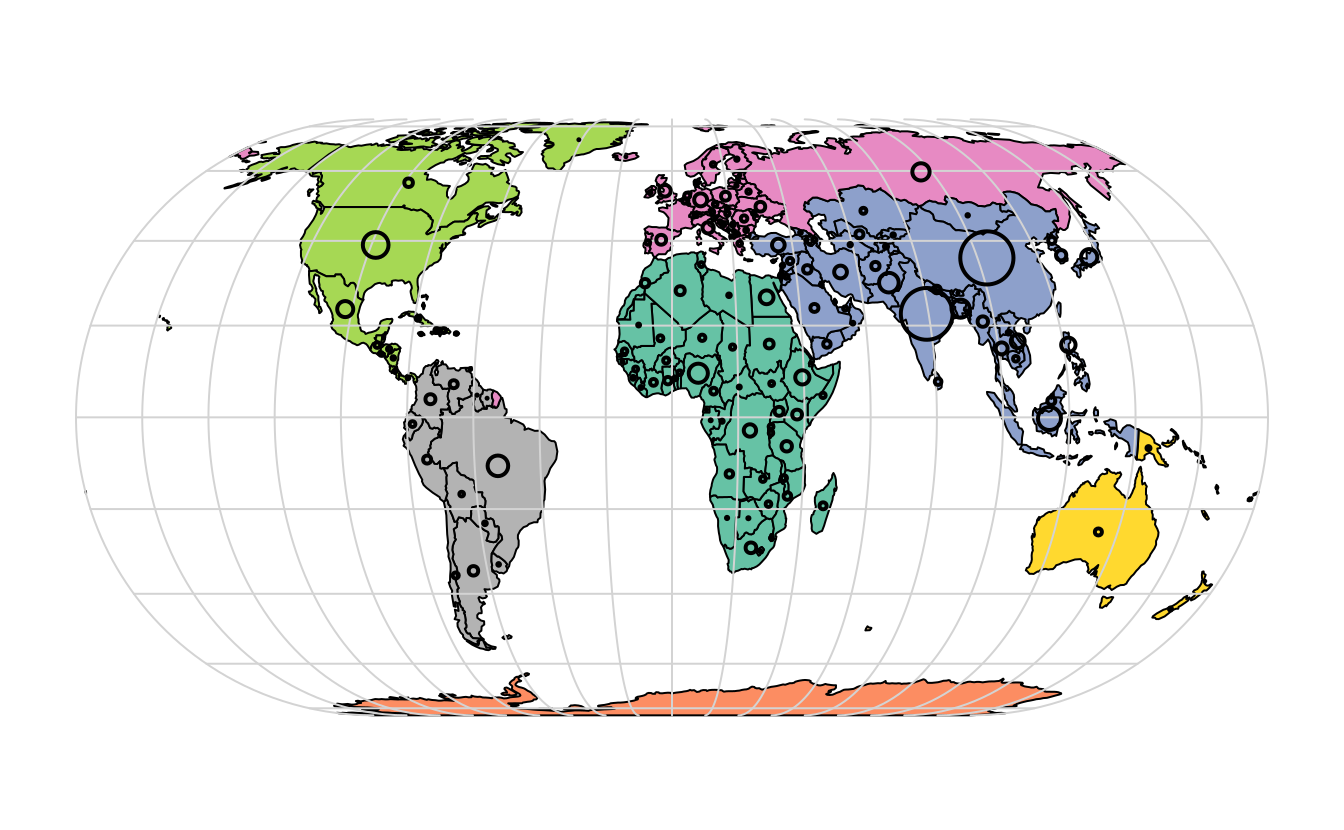

FIGURE 2.5: Continentes por países (representados por colores) y poblaciones de 2015 (representadas por círculos, con área proporcional a su población).

El código anterior utiliza la función st_centroid() para convertir un tipo de geometría (polígonos) en otra (puntos) (véase el capítulo ??), cuya estética se modifica mediante el argumento cex.

El método de graficación de sf también tiene argumentos específicos para los datos geográficos. expandBB, por ejemplo, puede usarse para representar un objeto sf en su contexto: toma un vector numérico de longitud cuatro que expande el contorno del gráfico relativo a cero en el siguiente orden: abajo, izquierda, arriba, derecha. Esto se utiliza para dibujar India en el contexto de sus gigantescos vecinos asiáticos, con énfasis en China al este, en el siguiente fragmento de código, que genera la Figura 2.6 (véanse los ejercicios más adelante sobre la adición de texto a los gráficos):

india = world[world$name_long == "India", ]
plot(st_geometry(india), expandBB = c(0, 0.2, 0.1, 1), col = "gray", lwd = 3)
plot(world_asia[0], add = TRUE)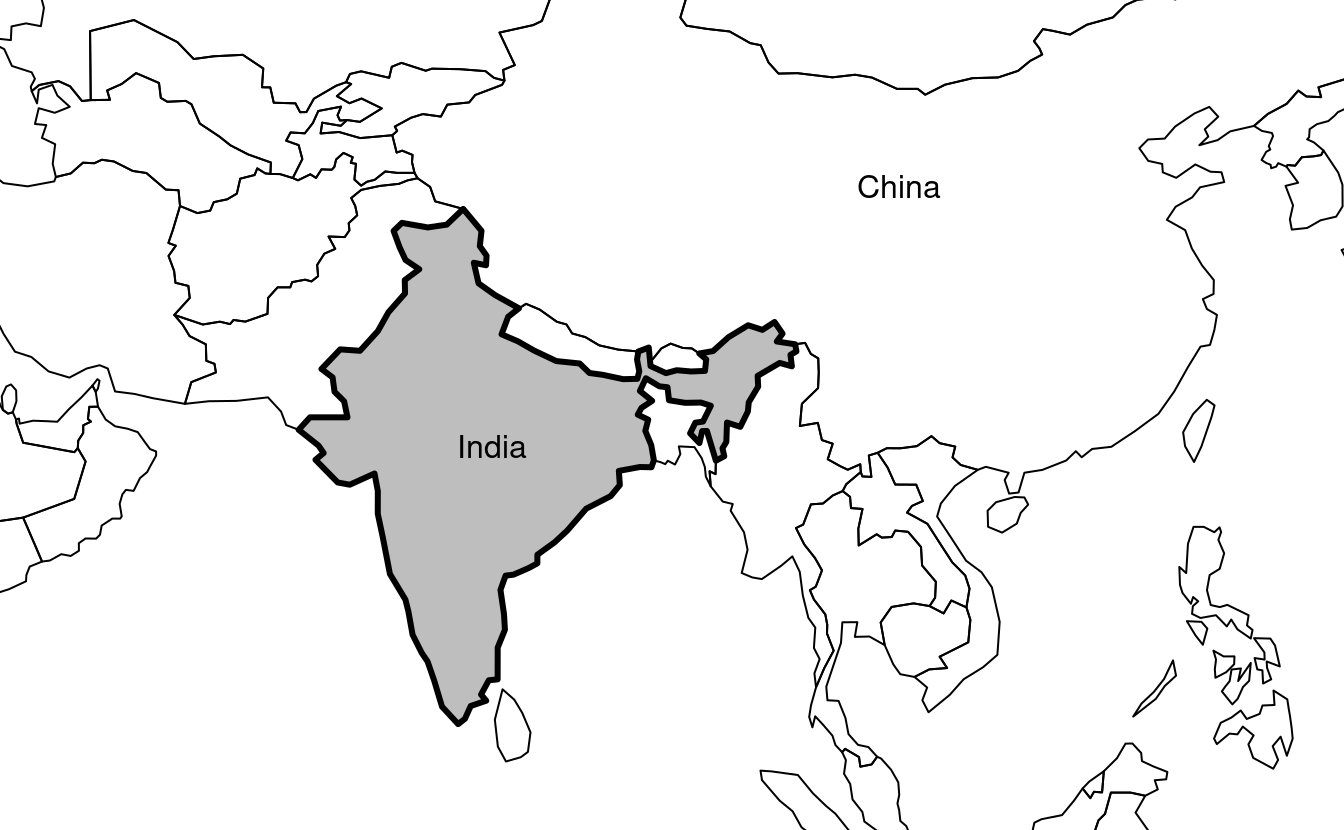

FIGURE 2.6: India en su contexto, mostrando el resultado del argumento expandBB.

Nótese el uso de [0] para mantener sólo la columna de geometría y lwd para enfatizar India. Véase la sección ?? para otras técnicas de visualización para representar distintos tipos de geometrías, el tema de la siguiente sección.

2.2.5 Tipos de geometrías

Las geometrías son los componentes básicos de Simple features. Simple features en R pueden adoptar uno de los 17 tipos de geometría compatibles con el paquete sf. En este capítulo nos centraremos en los siete tipos más utilizados: PUNTO, LÍNEA, POLÍGONO, MULTIPUNTO, MULTILÍNEA, MULTIPOLÍGONO y COLECCIÓN GEOMÉTRICA. Encontrarás la lista completa de tipos disponibles en el manual de PostGIS.

Por lo general, la codificación estándar para Simple features es la binaria conocida (well-known binary en inglés (WKB)) o el texto conocido (well-known text en inglés (WKT)). Las representaciones de WKB suelen ser cadenas hexadecimales fácilmente legibles para los ordenadores. Por ello, los SIG y las bases de datos espaciales utilizan WKB para transferir y almacenar objetos geométricos. WKT, por otra parte, es una descripción de texto legible para el ser humano de Simple features. Ambos formatos son intercambiables, y si debemos presentar uno, naturalmente elegiremos la representación WKT.

Las bases de cada tipo de geometría son los puntos. Un punto es simplemente una coordenada en el espacio 2D, 3D o 4D (véase vignette("sf1") para más información) así como (véase el panel izquierdo de la figura 2.7):

• POINT (5 2)

Una cadena de líneas es una secuencia de puntos con una línea recta que los une, por ejemplo (véase el panel central de la figura 2.7):

• LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2)

Un polígono es una secuencia de puntos que forman un anillo cerrado y sin intersecciones. Cerrado significa que el primer y el último punto de un polígono tienen las mismas coordenadas (véase el panel derecho de la figura 2.7).[ Por definición, un polígono tiene un límite exterior (anillo exterior) y puede tener cero o más límites interiores (anillos interiores), también conocidos como agujeros. Un polígono con agujeros serían, por ejemplo, POLYGON ((1 5, 2 2, 4 1, 4 4, 1 5), (2 4, 3 4, 3 3, 2 3, 2 4))]

• Polígono cerrado: POLYGON ((1 5, 2 2, 4 1, 4 4, 1 5))

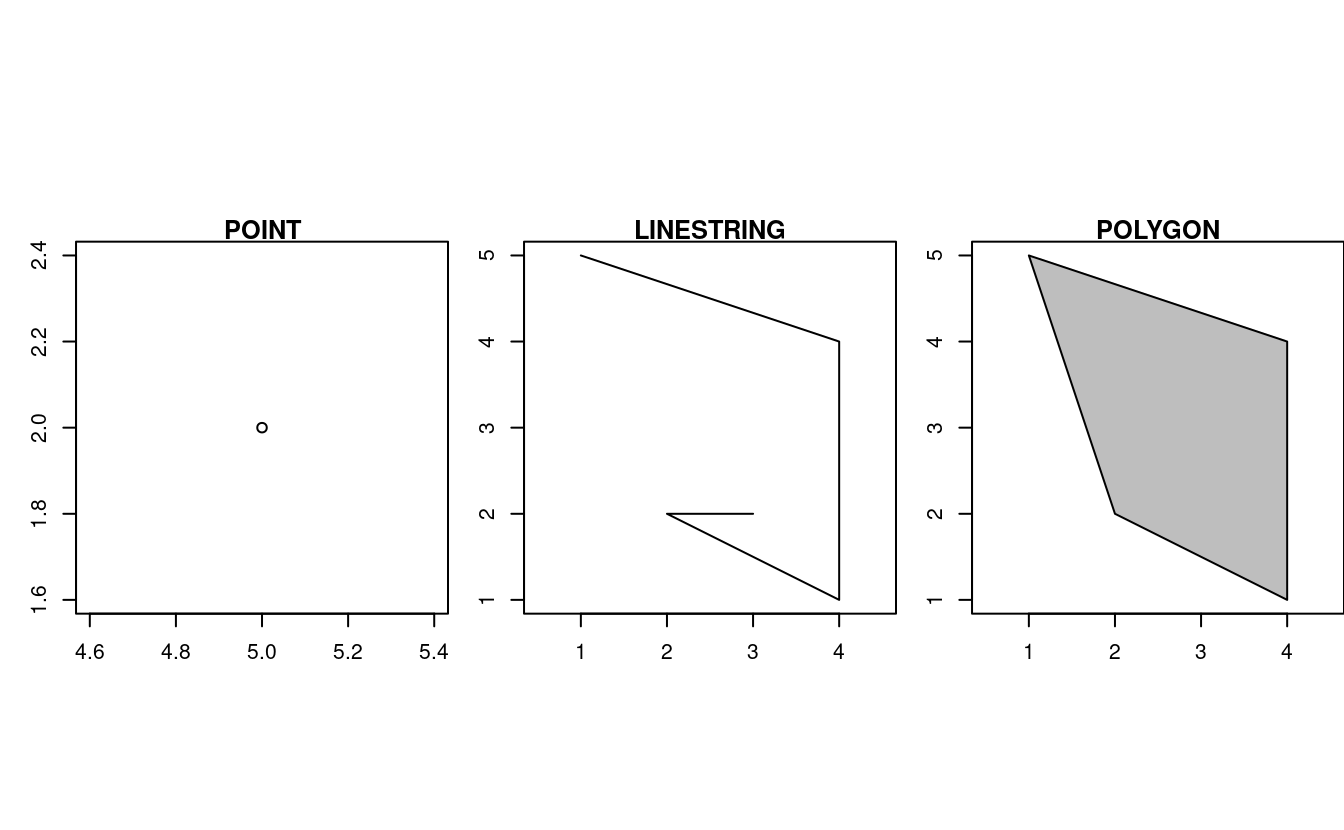
FIGURE 2.7: Ilustración de geometrías de puntos, líneas y polígonos.

Hasta ahora hemos creado geometrías con una sola entidad geométrica por objeto. Sin embargo, sf también permite la existencia de múltiples geometrías dentro de un único elemento (de ahí el término “colección de geometrías”) utilizando la versión “multi” de cada tipo de geometría:

• Multipunto: MULTIPOINT (5 2, 1 3, 3 4, 3 2)
• Multilínea: MULTILINESTRING ((1 5, 4 4, 4 1, 2 2, 3 2), (1 2, 2 4))
• Multipolígono: MULTIPOLYGON (((1 5, 2 2, 4 1, 4 4, 1 5), (0 2, 1 2, 1 3, 0 3, 0 2)))

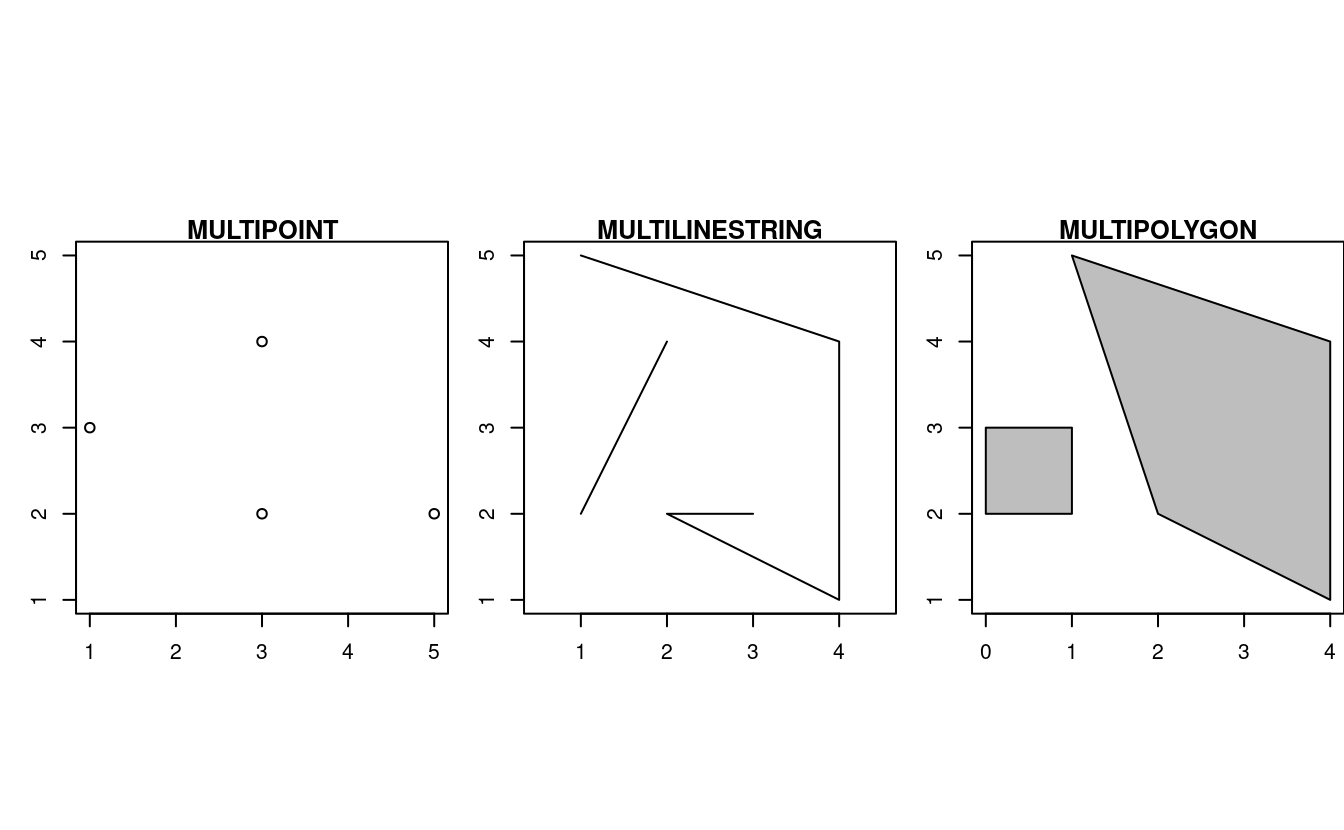
FIGURE 2.8: Illustration of multi* geometries.

Por último, una colección de geometrías puede contener cualquier combinación de geometrías, incluidos (multi)puntos y cadenas de líneas (véase la figura 2.9):

• Colección de geometrías: GEOMETRYCOLLECTION (MULTIPOINT (5 2, 1 3, 3 4, 3 2), LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2))

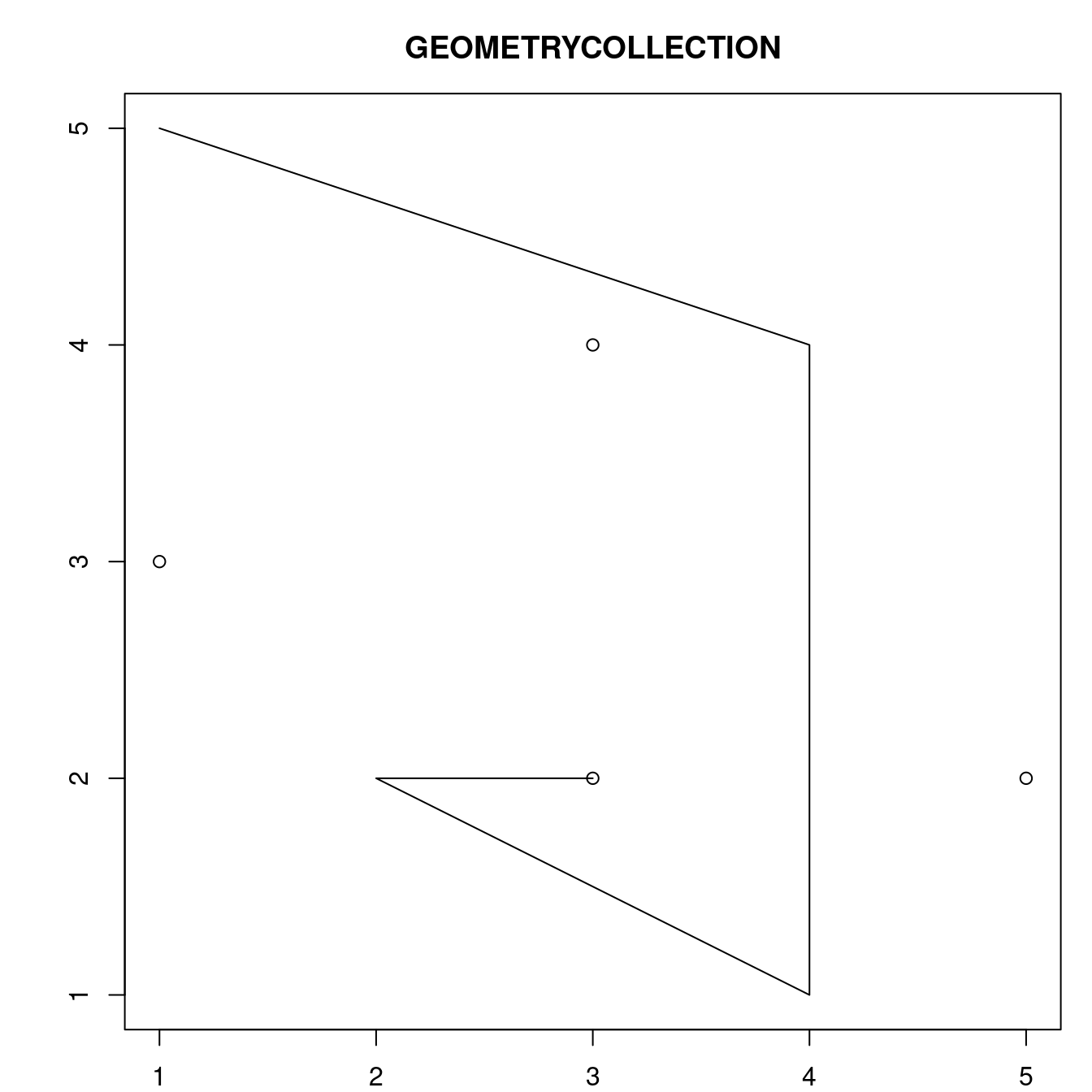
FIGURE 2.9: Ilustración de una colección de geometrías.

2.2.6 Geometrías de Simple features (sfg)

La clase sfg (Simple feature geometry en inglés) representa los diferentes tipos de geometrías de Simple features en R: punto, línea, polígono (y sus equivalentes ‘multi’, como multipuntos) o colección de geometrías.

Por lo general, te ahorras la tediosa tarea de crear geometrías por tu cuenta, ya que puedes simplemente importar un archivo espacial ya existente. Sin embargo, existe un conjunto de funciones para crear objetos sfg desde cero si es necesario. Los nombres de estas funciones son sencillos y coherentes, ya que todas comienzan con el prefijo st_ y terminan con el nombre del tipo de geometría en minúsculas:

• Punto: st_point()
• Línea: st_linestring()
• Polígono: st_polygon()
• Multipunto: st_multipoint()
• Multilínea: st_multilinestring()
• Multipolígono: st_multipolygon()
• Colección geométrica: st_geometrycollection()

Los objetos sfg pueden crearse a partir de tres tipos de datos básicos de R:

1. Un vector numérico: un solo punto
2. Una matriz: un conjunto de puntos, donde cada fila representa un punto, un multipunto o una línea
3. Una lista: una colección de objetos como matrices, multilíneas o colecciones de geometrías

La función st_point() crea puntos únicos a partir de vectores numéricos:

st_point(c(5, 2))                 # XY point
#> POINT (5 2)
st_point(c(5, 2, 3))              # XYZ point
#> POINT Z (5 2 3)
st_point(c(5, 2, 1), dim = "XYM") # XYM point
#> POINT M (5 2 1)
st_point(c(5, 2, 3, 1))           # XYZM point
#> POINT ZM (5 2 3 1)

Los resultados muestran que los tipos de punto XY (coordenadas 2D), XYZ (coordenadas 3D) y XYZM (3D con una variable adicional, normalmente la precisión de la medición) se crean a partir de vectores de longitud 2, 3 y 4, respectivamente. El tipo XYM debe especificarse mediante el argumento dim (que es la abreviatura de dimensión).

Por el contrario, utiliza matrices en el caso de los objetos multipunto (st_multipoint()) y en líneas (st_linestring()):

# la función rbind simplifica la creación de matrices
## MULTIPUNTO
multipoint_matrix = rbind(c(5, 2), c(1, 3), c(3, 4), c(3, 2))
st_multipoint(multipoint_matrix)
#> MULTIPOINT ((5 2), (1 3), (3 4), (3 2))
## LÍNEA
linestring_matrix = rbind(c(1, 5), c(4, 4), c(4, 1), c(2, 2), c(3, 2))
st_linestring(linestring_matrix)
#> LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2)

Por último, utiliza listas para la creación de multilíneas, (multi)polígonos y colecciones de geometrías:

## POLÍGONO
polygon_list = list(rbind(c(1, 5), c(2, 2), c(4, 1), c(4, 4), c(1, 5)))
st_polygon(polygon_list)
#> POLYGON ((1 5, 2 2, 4 1, 4 4, 1 5))

## POLÍGONO no cerrado
polygon_border = rbind(c(1, 5), c(2, 2), c(4, 1), c(4, 4), c(1, 5))
polygon_hole = rbind(c(2, 4), c(3, 4), c(3, 3), c(2, 3), c(2, 4))
polygon_with_hole_list = list(polygon_border, polygon_hole)
st_polygon(polygon_with_hole_list)
#> POLYGON ((1 5, 2 2, 4 1, 4 4, 1 5), (2 4, 3 4, 3 3, 2 3, 2 4))

## MULTILÍNEA
multilinestring_list = list(rbind(c(1, 5), c(4, 4), c(4, 1), c(2, 2), c(3, 2)), 
                            rbind(c(1, 2), c(2, 4)))
st_multilinestring((multilinestring_list))
#> MULTILINESTRING ((1 5, 4 4, 4 1, 2 2, 3 2), (1 2, 2 4))

## MULTIPOLÍGONO
multipolygon_list = list(list(rbind(c(1, 5), c(2, 2), c(4, 1), c(4, 4), c(1, 5))),
                         list(rbind(c(0, 2), c(1, 2), c(1, 3), c(0, 3), c(0, 2))))
st_multipolygon(multipolygon_list)
#> MULTIPOLYGON (((1 5, 2 2, 4 1, 4 4, 1 5)), ((0 2, 1 2, 1 3, 0 3, 0 2)))

## COLECCIÓN GEOMÉTRICA
gemetrycollection_list = list(st_multipoint(multipoint_matrix),
                              st_linestring(linestring_matrix))
st_geometrycollection(gemetrycollection_list)
#> GEOMETRYCOLLECTION (MULTIPOINT (5 2, 1 3, 3 4, 3 2),
#>   LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2))

2.2.7 Columnas de simple features (sfc)

Un objeto sfg contiene una sola geometría de Simple feature. Una columna de simple feature (Simple feature column en inglés (sfc)) es una lista de objetos sfg, que además puede contener información sobre el sistema de referencia de coordenadas en uso. Por ejemplo, para combinar dos objetos simple feature en un objeto con dos elementos, podemos utilizar la función st_sfc(). Esto es importante puesto que sfc representa la columna de geometría en los marcos de datos sf:

# PUNTO sfc 
point1 = st_point(c(5, 2))
point2 = st_point(c(1, 3))
points_sfc = st_sfc(point1, point2)
points_sfc
#> Geometry set for 2 features 
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: 1 ymin: 2 xmax: 5 ymax: 3
#> CRS:           NA
#> POINT (5 2)
#> POINT (1 3)

En la mayoría de los casos, un objeto sfc contiene objetos del mismo tipo de geometría. Por lo tanto, cuando convirtamos objetos sfg de tipo polígono en una columna de sfg, acabaríamos también con un objeto sfc de tipo polígono, lo cual puede verificarse con st_geometry_type(). Igualmente, una columna de geometría de multilíneas resultaría en un objeto sfc de tipo multilíneas:

# POLÍGONO sfc 
polygon_list1 = list(rbind(c(1, 5), c(2, 2), c(4, 1), c(4, 4), c(1, 5)))
polygon1 = st_polygon(polygon_list1)
polygon_list2 = list(rbind(c(0, 2), c(1, 2), c(1, 3), c(0, 3), c(0, 2)))
polygon2 = st_polygon(polygon_list2)
polygon_sfc = st_sfc(polygon1, polygon2)
st_geometry_type(polygon_sfc)
#> [1] POLYGON POLYGON
#> 18 Levels: GEOMETRY POINT LINESTRING POLYGON MULTIPOINT ... TRIANGLE

# MULTILÍNEA sfc 
multilinestring_list1 = list(rbind(c(1, 5), c(4, 4), c(4, 1), c(2, 2), c(3, 2)), 
                            rbind(c(1, 2), c(2, 4)))
multilinestring1 = st_multilinestring((multilinestring_list1))
multilinestring_list2 = list(rbind(c(2, 9), c(7, 9), c(5, 6), c(4, 7), c(2, 7)), 
                            rbind(c(1, 7), c(3, 8)))
multilinestring2 = st_multilinestring((multilinestring_list2))
multilinestring_sfc = st_sfc(multilinestring1, multilinestring2)
st_geometry_type(multilinestring_sfc)
#> [1] MULTILINESTRING MULTILINESTRING
#> 18 Levels: GEOMETRY POINT LINESTRING POLYGON MULTIPOINT ... TRIANGLE

También es posible crear un objeto sfc a partir de objetos sfg con diferentes tipos de geometrías:

# GEOMETRÍA sfc 
point_multilinestring_sfc = st_sfc(point1, multilinestring1)
st_geometry_type(point_multilinestring_sfc)
#> [1] POINT           MULTILINESTRING
#> 18 Levels: GEOMETRY POINT LINESTRING POLYGON MULTIPOINT ... TRIANGLE

Como se ha mencionado anteriormente, los objetos sfc pueden almacenar adicionalmente información sobre los sistemas de referencia de coordenadas (SRC). Para especificar un determinado SRC, podemos utilizar los atributos epsg (SRID) o proj4string de un objeto sfc. El valor por defecto de epsg (SRID) y proj4string es NA (No disponible o Not Available en inglés), como se puede comprobar con st_crs():

st_crs(points_sfc)
#> Coordinate Reference System: NA

Todas las geometrías de un objeto sfc deben tener el mismo SRC. Podemos añadir el sistema de referencia de coordenadas como argumento crs de st_sfc(). Este argumento acepta un número entero con el código epsg como 4326, el cual añade automáticamente el ‘proj4string’ (véase la sección 2.4):

# definición EPSG 
points_sfc_wgs = st_sfc(point1, point2, crs = 4326)
st_crs(points_sfc_wgs)
#> Coordinate Reference System:
#>   User input: EPSG:4326 
#>   wkt:
#> GEOGCRS["WGS 84",
#>     ENSEMBLE["World Geodetic System 1984 ensemble",
#>         MEMBER["World Geodetic System 1984 (Transit)"],
#>         MEMBER["World Geodetic System 1984 (G730)"],
#>         MEMBER["World Geodetic System 1984 (G873)"],
#>         MEMBER["World Geodetic System 1984 (G1150)"],
#>         MEMBER["World Geodetic System 1984 (G1674)"],
#>         MEMBER["World Geodetic System 1984 (G1762)"],
#>         MEMBER["World Geodetic System 1984 (G2139)"],
#>         ELLIPSOID["WGS 84",6378137,298.257223563,
#>             LENGTHUNIT["metre",1]],
#>         ENSEMBLEACCURACY[2.0]],
#>     PRIMEM["Greenwich",0,
#>         ANGLEUNIT["degree",0.0174532925199433]],
#>     CS[ellipsoidal,2],
#>         AXIS["geodetic latitude (Lat)",north,
#>             ORDER[1],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         AXIS["geodetic longitude (Lon)",east,
#>             ORDER[2],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>     USAGE[
#>         SCOPE["Horizontal component of 3D system."],
#>         AREA["World."],
#>         BBOX[-90,-180,90,180]],
#>     ID["EPSG",4326]]

También acepta un proj4string sin procesar (el resultado no se muestra):

# definición PROJ4STRING 
st_sfc(point1, point2, crs = "+proj=longlat +datum=WGS84 +no_defs")

A veces st_crs() devolverá un proj4string pero no un código epsg. Esto se debe a que no existe un método general para convertir de proj4string a epsg (véase el capítulo ??).

2.2.8 La clase sf

Los apartados 2.2.5 a 2.2.7 tratan de objetos puramente geométricos, ‘sf geometry’ y ‘sf column’ respectivamente. Estos son bloques de construcción geográficos de datos vectoriales geográficos representados como simple features. El último bloque de construcción son los atributos no geográficos, los cuales representan el nombre de la función u otros atributos como los valores medidos, los grupos y otras cosas.

Para ilustrar los atributos, representaremos una temperatura de 25°C en Londres el 21 de junio de 2017. Este ejemplo contiene una geometría (las coordenadas), y tres atributos con tres clases diferentes (nombre del lugar, temperatura y fecha).⁹ Los objetos de clase sf representan esos datos combinando los atributos (data.frame) con la columna de geometrías simple (sfc). Éstos son creados con st_sf() como se ilustra a continuación, lo cual crea el ejemplo de Londres descrito anteriormente:

lnd_point = st_point(c(0.1, 51.5))                 # objeto sfg 
lnd_geom = st_sfc(lnd_point, crs = 4326)           # objeto sfc 
lnd_attrib = data.frame(                           # objeto data.frame 
  name = "London",
  temperature = 25,
  date = as.Date("2017-06-21")
  )
lnd_sf = st_sf(lnd_attrib, geometry = lnd_geom)    # objeto sf 

¿Qué ha pasado? En primer lugar, las coordenadas se utilizaron para crear la geometría simple feature (sfg). En segundo lugar, la geometría se convirtió en una columna de geometrías simple feature (sfc), con un SRC. En tercer lugar, los atributos se almacenaron en un data.frame, que se combinó con el objeto sfc con st_sf(). Esto da como resultado un objeto sf, como se demuestra a continuación (se omiten algunos resultados):

lnd_sf
#> Simple feature collection with 1 features and 3 fields
#> ...
#>     name temperature       date         geometry
#> 1 London          25 2017-06-21 POINT (0.1 51.5)

class(lnd_sf)
#> [1] "sf"         "data.frame"

El resultado muestra que los objetos sf tienen en realidad dos clases, sf y data.frame. sf son simplemente marcos de datos (tablas cuadradas), pero con atributos espaciales almacenados en una columna con forma de lista, normalmente llamada geometría, como se describe en el apartado 2.2.1. Esta dualidad es fundamental para el concepto de simple features: la mayoría de las veces, un sf puede tratarse y comportarse como un data.frame. Simple features son, en esencia, marcos de datos con una extensión espacial.

2.3 Datos rasterizados

El modelo de datos espaciales rasterizados representa el mundo con la cuadrícula continua de celdas (a menudo también llamadas píxeles; 2.10:A). Este modelo de datos suele referirse a las llamadas cuadrículas regulares, en las que cada celda tiene el mismo tamaño constante, y en este libro nos centraremos únicamente en las cuadrículas regulares. Sin embargo, existen otros tipos de cuadrículas, como las cuadrículas rotadas, cizalladas, rectilíneas y curvilíneas (véase el capítulo 1 de Pebesma and Bivand (2022) o el capítulo 2 de Tennekes and Nowosad (2022))).

El modelo de datos ráster suele consistir en una cabecera ráster y una matriz (con filas y columnas) que representa celdas igualmente espaciadas (a menudo también llamadas píxeles; Figura 2.10:A).¹⁰ La cabecera ráster define el sistema de referencia de coordenadas, la extensión y el origen. El origen (o punto de partida) suele ser la coordenada de la esquina inferior izquierda de la matriz (el paquete terra, sin embargo, utiliza la esquina superior izquierda, por defecto (Figura 2.10:B)). La cabecera define la extensión mediante el número de columnas, el número de filas y la resolución del tamaño de las celdas. Por lo tanto, partiendo del origen, podemos acceder fácilmente a cada celda y modificarla utilizando su ID (Figura 2.10:B) o especificando explícitamente las filas y las columnas. Esta representación matricial evita almacenar explícitamente las coordenadas de los cuatro puntos de las esquinas (de hecho, sólo almacena una coordenada, el origen) de cada celda, como ocurriría con los polígonos vectoriales rectangulares. Esto y el álgebra de mapas (apartado (map-algebra)) hacen que el procesamiento de rásters sea mucho más eficiente y rápido que el de datos vectoriales. Sin embargo, a diferencia de los datos vectoriales, la celda de una capa ráster sólo puede contener un único valor. El valor puede ser numérico o categórico (Figura 2.10:C).

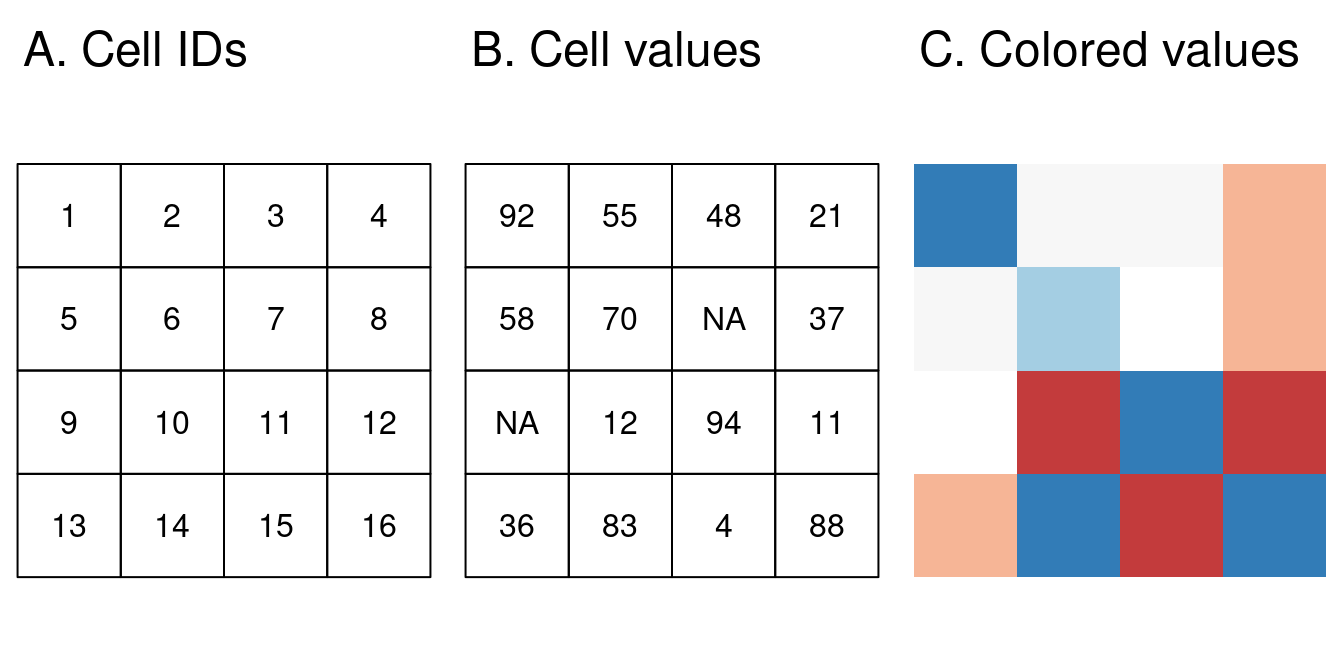
FIGURE 2.10: Tipos de datos ráster: (A) IDs de celdas, (B) valores de celdas, (C) un mapa raster coloreado.

Los mapas ráster suelen representar fenómenos continuos como la elevación, la temperatura, la densidad de población o los datos espectrales (Figura 2.11). Por supuesto, también podemos representar características discretas, como las clases de suelo o de cobertura del suelo, con la ayuda de un modelo de datos raster (Figura 2.11). En consecuencia, los límites discretos de estas características se difuminan y, dependiendo de la tarea espacial, podría ser más adecuada una representación vectorial.

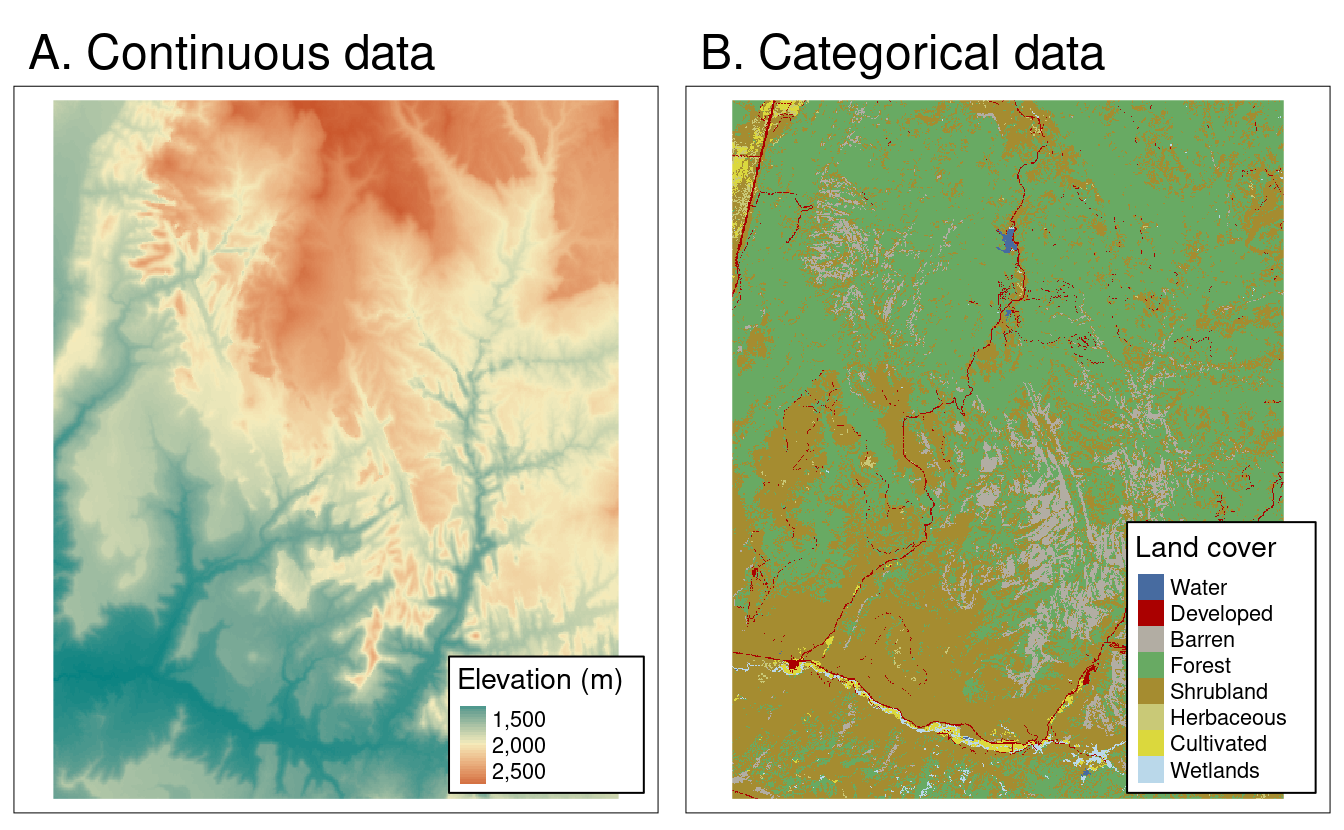
FIGURE 2.11: Ejemplos de rásters continuos y categóricos.

2.3.1 Paquetes de R para el manejo de datos rasterizados

2.3.2 Introducción a terra

El paquete terra soporta objetos raster en R. Proporciona un amplio conjunto de funciones para crear, leer, exportar, manipular y procesar conjuntos de datos raster. Aparte de la manipulación general de datos ráster, terra proporciona muchas funciones de bajo nivel que pueden constituir la base para desarrollar una funcionalidad ráster más avanzada. terra también permite trabajar con grandes conjuntos de datos ráster que son demasiado grandes para caber en una memoria principal. En este caso, terra ofrece la posibilidad de dividir el raster en fragmentos más pequeños, y los procesa iterativamente en lugar de cargar todo el archivo raster en la RAM.

Para ilustrar los conceptos de terra, utilizaremos los conjuntos de datos de spDataLarge. Se trata de unos cuantos objetos ráster y un objeto vectorial que cubren una zona del Parque Nacional de Zion (Utah, EE.UU.). Por ejemplo, srtm.tif es un modelo digital de elevación de esta zona (para más detalles, véase su documentación con ?srtm). En primer lugar, vamos a crear un objeto SpatRaster llamado my_rast:

raster_filepath = system.file("raster/srtm.tif", package = "spDataLarge")
my_rast = rast(raster_filepath)

Al escribir el nombre del raster en la consola, el resultado será la cabecera del raster (dimensiones, resolución, extensión, SRC) y alguna información adicional (clase, fuente de datos, resumen de los valores del ráster):

my_rast
#> class       : SpatRaster 
#> dimensions  : 457, 465, 1  (nrow, ncol, nlyr)
#> resolution  : 0.000833, 0.000833  (x, y)
#> extent      : -113, -113, 37.1, 37.5  (xmin, xmax, ymin, ymax)
#> coord. ref. : lon/lat WGS 84 (EPSG:4326) 
#> source      : srtm.tif 
#> name        : srtm 
#> min value   : 1024 
#> max value   : 2892

Las funciones dedicadas informan de cada componente: dim(my_rast) retorna el número de filas, columnas y capas; ncell() el número de celdas (píxeles); res() la resolución espacial; ext() su extensión espacial; y crs() su sistema de referencia de coordenadas (la reproyección raster se trata en la Sección ??). inMemory() informa de si los datos raster están almacenados en memoria o en disco.

help("terra-package") retorna una lista completa de todas las funciones disponibles de terra

2.3.3 Elaboración de mapas básicos

Al igual que el paquete sf, terra también proporciona métodos plot() para sus propias clases.

plot(my_rast)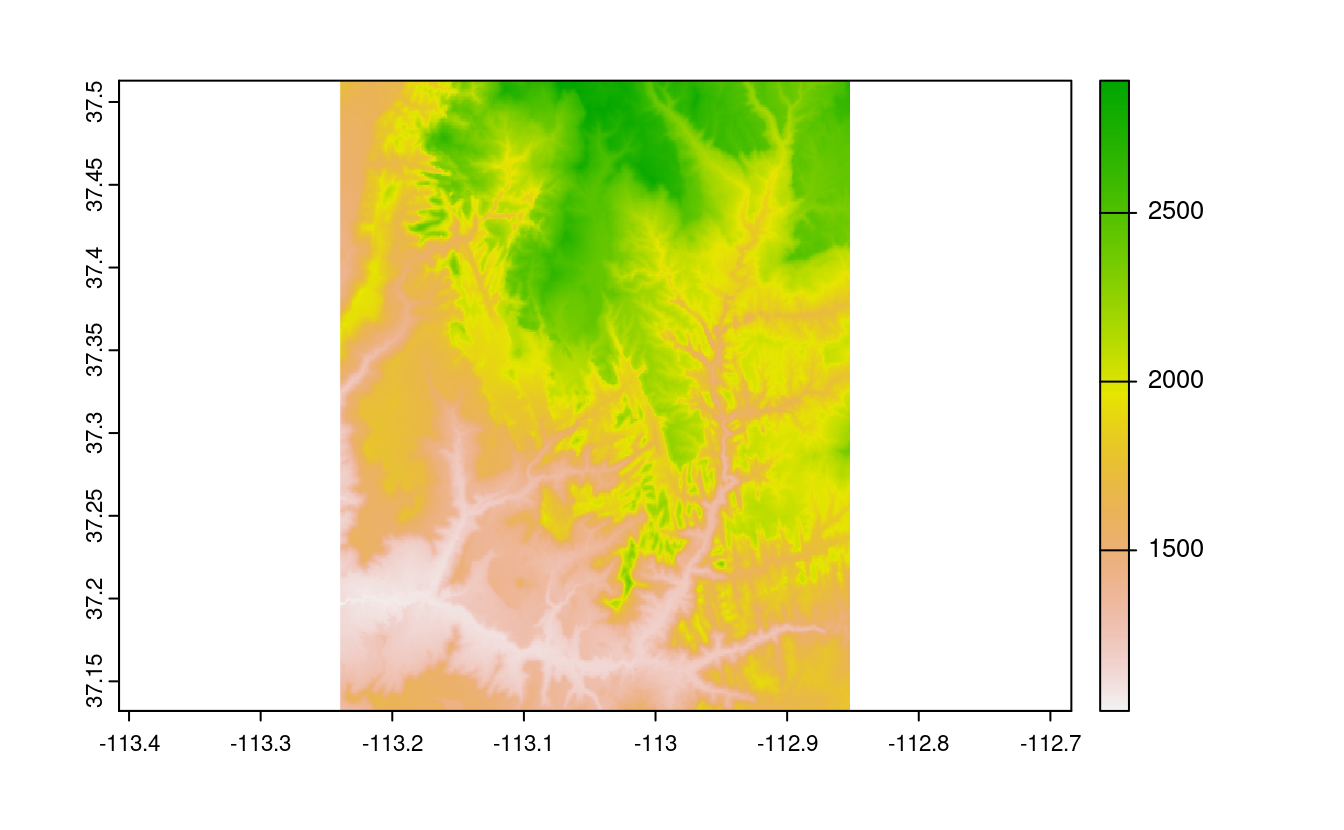

FIGURE 2.12: Gráfico raster básico.

Existen otros enfoques para representar datos ráster en R que quedan fuera del alcance de esta sección, por ejemplo:

• paquetes como tmap para crear mapas estáticos e interactivos de objetos raster y vectoriales (véase el capítulo ??)
• funciones, por ejemplo levelplot() del paquete rasterVis, para crear facetas, una técnica común para visualizar el cambio en el tiempo

2.3.4 Clases ráster

La clase SpatRaster representa un objeto raster en terra. La forma más fácil de crear un objeto raster en R es leer un archivo raster desde el disco o desde un servidor (Sección ??).

single_raster_file = system.file("raster/srtm.tif", package = "spDataLarge")
single_rast = rast(raster_filepath)

El paquete terra soporta numerosos controles con la ayuda de la librería GDAL. Los rásters de los archivos no suelen ser leídos en su totalidad en la memoria RAM, a excepción de su cabecera y un puntero al propio archivo.

Los rásters también pueden crearse desde cero utilizando la misma función rast(). Esto se ilustra en el siguiente fragmento de código, que da como resultado un nuevo objeto SpatRaster. El raster resultante consta de 36 celdas (6 columnas y 6 filas especificadas por nrows y ncols) centradas alrededor del Primer Meridiano y el Ecuador (ver parámetros xmin, xmax, ymin y ymax). El SRC por defecto de los objetos ráster es WGS84, pero puede cambiarse con el argumento crs. Esto significa que la unidad de la resolución está en grados, que fijamos en 0,5 (resolución). Los valores (vals) se asignan a cada celda: 1 a la celda 1, 2 a la celda 2, y así sucesivamente. Recuerda: rast() rellena las celdas por filas (a diferencia de matrix()) empezando por la esquina superior izquierda, lo que significa que la fila superior contiene los valores del 1 al 6, la segunda del 7 al 12, etc.

new_raster = rast(nrows = 6, ncols = 6, resolution = 0.5, 
                  xmin = -1.5, xmax = 1.5, ymin = -1.5, ymax = 1.5,
                  vals = 1:36)

Para otras formas de crear objetos ráster, véase ?rast.

La clase SpatRaster también maneja múltiples capas, que suelen corresponder a un único archivo de satélite multiespectral o a una serie temporal de rásters.

multi_raster_file = system.file("raster/landsat.tif", package = "spDataLarge")
multi_rast = rast(multi_raster_file)

multi_rast
#> class       : SpatRaster 
#> dimensions  : 1428, 1128, 4  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : 301905, 335745, 4111245, 4154085  (xmin, xmax, ymin, ymax)
#> coord. ref. : WGS 84 / UTM zone 12N (EPSG:32612) 
#> source      : landsat.tif 
#> names       : landsat_1, landsat_2, landsat_3, landsat_4 
#> min values  :      7550,      6404,      5678,      5252 
#> max values  :     19071,     22051,     25780,     31961

nlyr() recupera el número de capas almacenadas en un objeto ‘SpatRaster’:

nlyr(multi_rast)
#> [1] 4

2.4 Sistemas de referencia de coordenadas

Los tipos de datos espaciales vectoriales y ráster comparten conceptos intrínsecos a los datos espaciales. Quizás el más fundamental sea el Sistema de Referencia de Coordenadas (SRC), que define cómo se relacionan los elementos espaciales de los datos con la superficie de la Tierra (u otros cuerpos). Los SRC son geográficos o proyectados, tal y como se ha introducido al principio de este capítulo (véase la figura 2.1). En esta sección se explicará cada tipo, sentando las bases para la Sección ?? sobre transformaciones de SRC.

2.4.1 Sistemas de coordenadas geográficas

Los sistemas de coordenadas geográficas identifican cualquier ubicación en la superficie de la Tierra mediante dos valores: la longitud y la latitud (véase el panel izquierdo de la figura 2.13 y 2.14). La longitud es la ubicación en la dirección Este-Oeste en distancia angular desde el plano del Primer Meridiano (también conocido como Meridiano de Greenwich). La latitud es la distancia angular al Norte o al Sur del plano ecuatorial. Por tanto, las distancias en los SRC geográficos no se miden en metros. Esto tiene importantes consecuencias, como se demuestra en el capítulo ??.

La superficie de la Tierra en los sistemas de coordenadas geográficas se representa mediante una superficie esférica o elipsoidal. Los modelos esféricos suponen que la Tierra es una esfera perfecta de un radio determinado; tienen la ventaja de la simplicidad pero, al mismo tiempo, son inexactos: ¡la Tierra no es una esfera! Los modelos elipsoidales se definen mediante dos parámetros: el radio ecuatorial y el radio polar. Éstos son adecuados porque la Tierra está comprimida: el radio ecuatorial es unos 11,5 km más largo que el radio polar (Maling 1992).^[

El grado de compresión se suele denominar aplanamiento, definido en función del radio ecuatorial (\(a\)) y el radio polar (\(b\)) de la siguiente manera \(f = (a - b) / a\). También se pueden utilizar los términos elipticidad y compresión. Debido a que \(f\) es un valor bastante pequeño, los modelos de elipsoides digitales utilizan el “aplanamiento inverso” (\(rf = 1/f\)) para definir la compresión de la Tierra. Los valores de \(a\) y \(rf\) en varios modelos elipsoidales pueden verse ejecutando sf_proj_info(type = "ellps"). ]

Los elipsoides forman parte de un componente más amplio de los SRC: el datum. Éste contiene información sobre el elipsoide que debe utilizarse y la relación precisa entre las coordenadas cartesianas y la ubicación en la superficie de la Tierra.

Hay dos tipos de datum: geocéntrico y local. En un dato geocéntrico, como el WGS84, el centro es el centro de gravedad de la Tierra y la precisión de las proyecciones no está optimizada para una ubicación específica. En un dato local, como el NAD83, la superficie elipsoidal se desplaza para alinearse con la superficie de un lugar concreto.

2.4.2 Sistemas de referencia de coordenadas proyectadas

Los SRC proyectados se basan en coordenadas cartesianas sobre una superficie implícitamente plana (panel derecho de las Figuras 2.13 y 2.14). Tienen un origen, unos ejes x e y y una unidad de medida lineal como los metros. Todos los SRC proyectados se basan en un SRC geográfico, descrito en la sección anterior, y se apoyan en proyecciones cartográficas para convertir la superficie tridimensional de la Tierra en valores de Este y Norte (x e y) en un SRC proyectado.

Esta transición no puede realizarse sin añadir algunas deformaciones. Por tanto, algunas propiedades de la superficie terrestre se distorsionan en este proceso, como el área, la dirección, la distancia y la forma. Un sistema de coordenadas proyectado puede conservar sólo una o dos de esas propiedades. Las proyecciones suelen denominarse en función de la propiedad que preservan: las de áreas iguales preservan el área, la azimutal preserva la dirección, la equidistante preserva la distancia y la conformal preserva la forma local.

Existen tres grupos principales de tipos de proyección: cónica, cilíndrica y planar (azimutal). En una proyección cónica, la superficie de la Tierra se proyecta en un cono a lo largo de una única línea de tangencia o de dos líneas de tangencia. Las distorsiones se minimizan a lo largo de las líneas de tangencia y aumentan con la distancia desde esas líneas en esta proyección. Por lo tanto, es la más adecuada para los mapas de zonas de latitud media. Una proyección cilíndrica representa la superficie en un cilindro. Esta proyección también puede crearse tocando la superficie de la Tierra a lo largo de una sola línea de tangencia o de dos líneas de tangencia. Las proyecciones cilíndricas son las que más se utilizan para cartografiar el mundo en su totalidad. Una proyección plana proyecta los datos sobre una superficie plana que toca el globo en un punto o a lo largo de una línea de tangencia. Se suele utilizar para cartografiar regiones polares. sf_proj_info(type = "proj") ofrece una lista de las proyecciones disponibles que admite la librería PROJ.

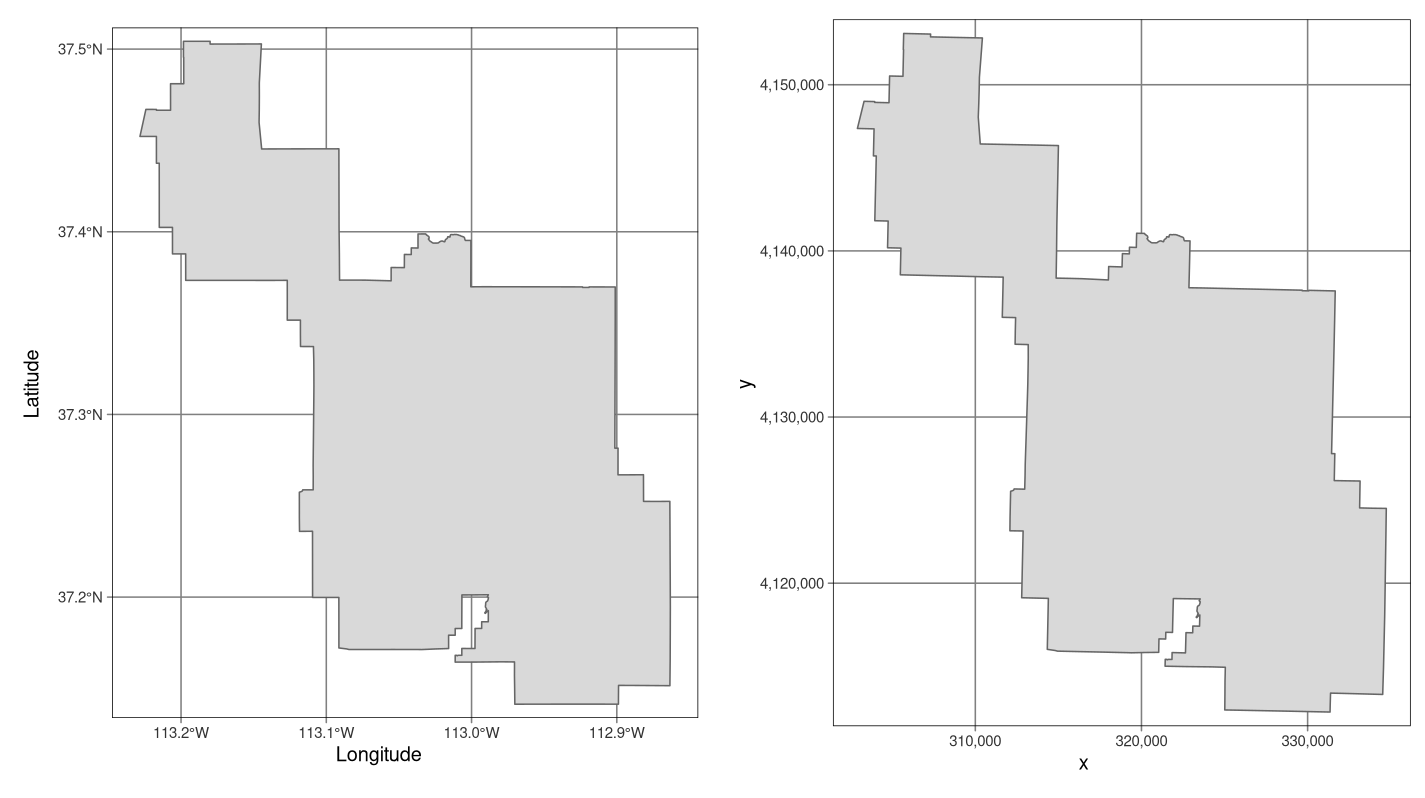
FIGURE 2.13: Ejemplos de sistemas de coordenadas geográficas (WGS 84; izquierda) y proyectadas (NAD83 / zona UTM 12N; derecha) para datos vectoriales.

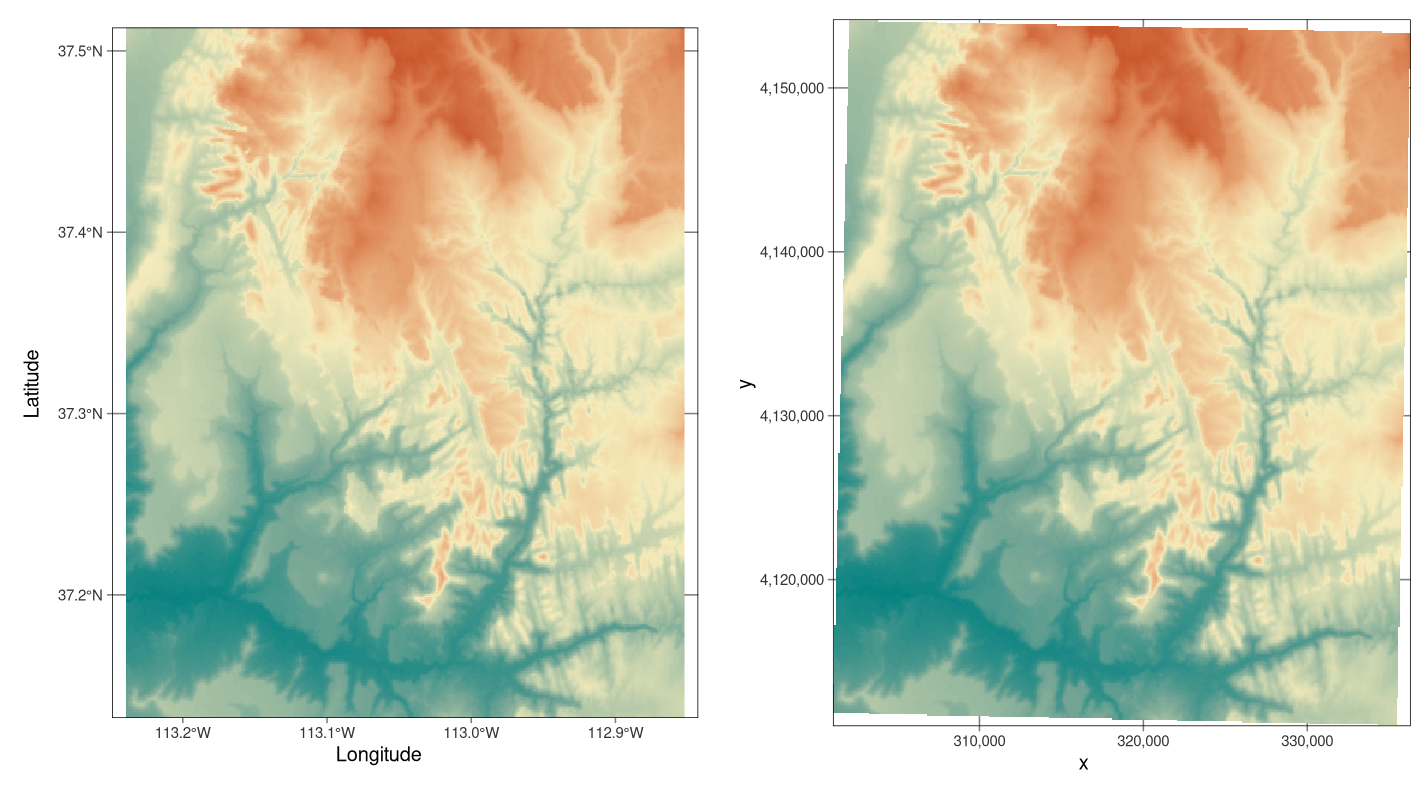
FIGURE 2.14: Ejemplos de sistemas de coordenadas geográficas (WGS 84; izquierda) y proyectadas (NAD83 / zona UTM 12N; derecha) para datos rasterizados.

2.4.3 SRC en R

Dos formas recomendables de describir los SRC en R son (a) los identificadores de sistemas de referencia espacial (Spatial Reference System Identifiers en inglés (SRID)) o (b) las definiciones de texto conocidas (WKT2). Ambos enfoques tienen ventajas y desventajas.

Un código epsg suele ser más corto y, por tanto, más fácil de recordar. El código también se refiere a un solo sistema de referencia de coordenadas bien definido.

Los paquetes espaciales de R admiten una amplia gama de SRC y utilizan la biblioteca PROJ, establecida desde hace tiempo.

En sf el SRC de un objeto puede ser recuperado usando st_crs(). Para ello, necesitamos leer un conjunto de datos vectoriales:

vector_filepath = system.file("vector/zion.gpkg", package = "spDataLarge")
new_vector = st_read(vector_filepath)

Nuestro nuevo objeto, new_vector, es un polígono que representa los límites del Parque Nacional de Zion (?zion).

st_crs(new_vector) # get CRS
#> Coordinate Reference System:
#>   User input: UTM Zone 12, Northern Hemisphere 
#>   wkt:
#> BOUNDCRS[
#>     SOURCECRS[
#>         PROJCRS["UTM Zone 12, Northern Hemisphere",
#>             BASEGEOGCRS["GRS 1980(IUGG, 1980)",
#>                 DATUM["unknown",
#>                     ELLIPSOID["GRS80",6378137,298.257222101,
#>                         LENGTHUNIT["metre",1,
#>                             ID["EPSG",9001]]]],
#>                 PRIMEM["Greenwich",0,
#>                     ANGLEUNIT["degree",0.0174532925199433]]],
#>             CONVERSION["UTM zone 12N",
#>                 METHOD["Transverse Mercator",
#>                     ID["EPSG",9807]],
#>                 PARAMETER["Latitude of natural origin",0,
#>                     ANGLEUNIT["degree",0.0174532925199433],
#>                     ID["EPSG",8801]],
#>                 PARAMETER["Longitude of natural origin",-111,
#>                     ANGLEUNIT["degree",0.0174532925199433],
#>                     ID["EPSG",8802]],
#>                 PARAMETER["Scale factor at natural origin",0.9996,
#>                     SCALEUNIT["unity",1],
#>                     ID["EPSG",8805]],
#>                 PARAMETER["False easting",500000,
#>                     LENGTHUNIT["Meter",1],
#>                     ID["EPSG",8806]],
#>                 PARAMETER["False northing",0,
#>                     LENGTHUNIT["Meter",1],
#>                     ID["EPSG",8807]],
#>                 ID["EPSG",16012]],
#>             CS[Cartesian,2],
#>                 AXIS["(E)",east,
#>                     ORDER[1],
#>                     LENGTHUNIT["Meter",1]],
#>                 AXIS["(N)",north,
#>                     ORDER[2],
#>                     LENGTHUNIT["Meter",1]]]],
#>     TARGETCRS[
#>         GEOGCRS["WGS 84",
#>             DATUM["World Geodetic System 1984",
#>                 ELLIPSOID["WGS 84",6378137,298.257223563,
#>                     LENGTHUNIT["metre",1]]],
#>             PRIMEM["Greenwich",0,
#>                 ANGLEUNIT["degree",0.0174532925199433]],
#>             CS[ellipsoidal,2],
#>                 AXIS["latitude",north,
#>                     ORDER[1],
#>                     ANGLEUNIT["degree",0.0174532925199433]],
#>                 AXIS["longitude",east,
#>                     ORDER[2],
#>                     ANGLEUNIT["degree",0.0174532925199433]],
#>             ID["EPSG",4326]]],
#>     ABRIDGEDTRANSFORMATION["Transformation from GRS 1980(IUGG, 1980) to WGS84",
#>         METHOD["Position Vector transformation (geog2D domain)",
#>             ID["EPSG",9606]],
#>         PARAMETER["X-axis translation",0,
#>             ID["EPSG",8605]],
#>         PARAMETER["Y-axis translation",0,
#>             ID["EPSG",8606]],
#>         PARAMETER["Z-axis translation",0,
#>             ID["EPSG",8607]],
#>         PARAMETER["X-axis rotation",0,
#>             ID["EPSG",8608]],
#>         PARAMETER["Y-axis rotation",0,
#>             ID["EPSG",8609]],
#>         PARAMETER["Z-axis rotation",0,
#>             ID["EPSG",8610]],
#>         PARAMETER["Scale difference",1,
#>             ID["EPSG",8611]]]]

En los casos en que falta un sistema de referencia de coordenadas (SRC) o se establece un SRC incorrecto, se puede utilizar la función st_set_crs():

new_vector = st_set_crs(new_vector, "EPSG:26912") # set CRS
#> Warning: st_crs<- : replacing crs does not reproject data; use st_transform for
#> that

El mensaje de advertencia nos informa de que la función st_set_crs() no transforma los datos de un SRC a otro.

La función crs() se puede utilizar para acceder a la información del SRC desde un objeto SpatRaster:

crs(my_rast) # get CRS
#> [1] "GEOGCRS[\"WGS 84\",\n    DATUM[\"World Geodetic System 1984\",\n        ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n            LENGTHUNIT[\"metre\",1]]],\n    PRIMEM[\"Greenwich\",0,\n        ANGLEUNIT[\"degree\",0.0174532925199433]],\n    CS[ellipsoidal,2],\n        AXIS[\"geodetic latitude (Lat)\",north,\n            ORDER[1],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n        AXIS[\"geodetic longitude (Lon)\",east,\n            ORDER[2],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n    ID[\"EPSG\",4326]]"

La misma función, crs(), se utiliza para establecer un SRC para los objetos raster.

my_rast2 = my_rast
crs(my_rast2) = "EPSG:26912" # set CRS

Es importante destacar que las funciones st_crs() y crs() no alteran los valores de las coordenadas ni las geometrías. Su función es sólo la de establecer los metadatos sobre el objeto SRC. Ampliaremos los SRC y explicaremos cómo proyectar de un SRC a otro en el capítulo ??.

2.5 Paquete Units

Una característica importante de los SRC es que contienen información sobre las unidades espaciales. Está claro que es vital saber si las medidas de una casa están en pies o en metros, y lo mismo ocurre con los mapas. Es una buena práctica cartográfica añadir una barra de escala o algún otro indicador de distancia en los mapas para demostrar la relación entre las distancias en la página o la pantalla y las distancias sobre el terreno. Del mismo modo, es importante especificar formalmente las unidades en las que se miden los datos geométricos o las celdas para proporcionar un contexto, y garantizar que los cálculos posteriores se realicen en contexto.

Una característica novedosa de los datos geométricos en los objetos sf es que tienen soporte nativo para las unidades. Esto significa que la distancia, el área y otros cálculos geométricos en sf devuelven valores que vienen con un atributo de unidades, definido por el paquete Units (Pebesma, Mailund, and Hiebert 2016). Esto es ventajoso, ya que evita la confusión causada por las diferentes unidades (la mayoría de los SRC utilizan metros, algunos utilizan pies) y proporciona información sobre la dimensionalidad. Esto se demuestra en el siguiente fragmento de código, que calcula la superficie de Luxemburgo:

luxembourg = world[world$name_long == "Luxembourg", ]

st_area(luxembourg) # requiere del paquete s2 en versiones recientes de sf
#> 2.41e+09 [m^2]

El resultado está en unidades de metros cuadrados (m²), lo que demuestra que el resultado representa un espacio bidimensional. Esta información, almacenada como un atributo (que los lectores interesados pueden descubrir con attributes(st_area(luxembourg))), puede aportar a cálculos posteriores que utilicen unidades, como la densidad de población (que se mide en personas por unidad de superficie, normalmente por km²). Informar de las unidades evita confusiones. Por ejemplo, en el caso de Luxemburgo, si no se especificaran las unidades, se podría suponer erróneamente que se trata de hectáreas. Para traducir la enorme cifra a un tamaño más digerible, resulta tentador dividir los resultados por un millón (el número de metros cuadrados en un kilómetro cuadrado):

st_area(luxembourg) / 1000000
#> 2409 [m^2]

Sin embargo, el resultado se vuelve a dar incorrectamente como metros cuadrados. La solución es establecer las unidades correctas con el paquete Units:

units::set_units(st_area(luxembourg), km^2)
#> 2409 [km^2]

Las unidades tienen la misma importancia en el caso de los datos ráster. Sin embargo, hasta ahora sf es el único paquete espacial que soporta unidades, lo que significa que las personas que trabajan con datos ráster deben abordar los cambios en las unidades de análisis (por ejemplo, la conversión de la anchura de los píxeles de unidades imperiales a decimales) con cuidado. El objeto my_rast (véase más arriba) utiliza una proyección WGS84 con grados decimales como unidades. En consecuencia, su resolución también se da en grados decimales, pero hay que conocerla, ya que la función res() simplemente devuelve un vector numérico.

res(my_rast)
#> [1] 0.000833 0.000833

Si utilizáramos la proyección UTM, las unidades cambiarían.

repr = project(my_rast, "EPSG:26912")
res(repr)

De nuevo, el comando res() devuelve un vector numérico sin ninguna unidad, lo que nos obliga a saber que la unidad de la proyección UTM es el metro.

2.6 Ejercicios