6 Raster-vector interactions
6.1 Introduction
This chapter focuses on interactions between raster and vector geographic data models, introduced in Chapter 2. It includes several main techniques: raster cropping and masking using vector objects (Section 6.2), extracting raster values using different types of vector data (Section 6.3), and raster-vector conversion (Sections 6.4 and 6.5). The above concepts are demonstrated using data from previous chapters to understand their potential real-world applications.
6.2 Raster cropping
Many geographic data projects involve integrating data from many different sources, such as remote sensing images (rasters) and administrative boundaries (vectors). Often the extent of input raster datasets is larger than the area of interest. In this case, raster cropping and masking are useful for unifying the spatial extent of input data. Both operations reduce object memory use and associated computational resources for subsequent analysis steps and may be a necessary preprocessing step when creating attractive maps involving raster data.
We will use two objects to illustrate raster cropping:
- A
SpatRasterobjectsrtmrepresenting elevation (meters above sea level) in southwestern Utah - A vector (
sf) objectzionrepresenting Zion National Park
Both target and cropping objects must have the same projection.
The following code chunk therefore not only reads the datasets from the spDataLarge package installed in Chapter 2, but it also ‘reprojects’ zion (a topic covered in Chapter 7):
srtm = rast(system.file("raster/srtm.tif", package = "spDataLarge"))
zion = read_sf(system.file("vector/zion.gpkg", package = "spDataLarge"))
zion = st_transform(zion, st_crs(srtm))We use crop() from the terra package to crop the srtm raster.
The function reduces the rectangular extent of the object passed to its first argument based on the extent of the object passed to its second argument.
This functionality is demonstrated in the command below, which generates Figure 6.1(B).
srtm_cropped = crop(srtm, zion)
Related to crop() is the terra function mask(), which sets values outside of the bounds of the object passed to its second argument to NA.
The following command therefore masks every cell outside of Zion National Park boundaries (Figure 6.1(C)).
srtm_masked = mask(srtm, zion)Importantly, we want to use both crop() and mask() together in most cases.
This combination of functions would (a) limit the raster’s extent to our area of interest and then (b) replace all of the values outside of the area to NA.27
Changing the settings of mask() yields different results.
Setting inverse = TRUE will mask everything inside the bounds of the park (see ?mask for details) (Figure 6.1(D)), while setting updatevalue = 0 will set all pixels outside the national park to 0.
srtm_inv_masked = mask(srtm, zion, inverse = TRUE)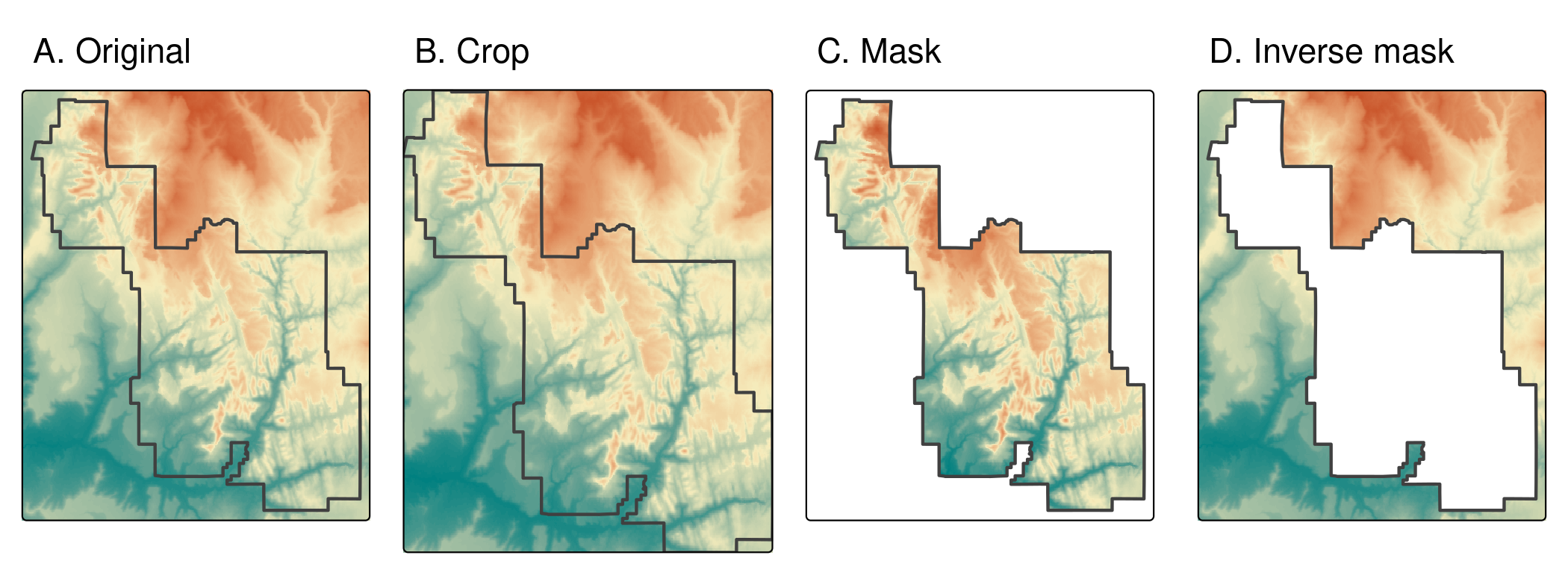
FIGURE 6.1: Raster cropping and raster masking.
6.3 Raster extraction
Raster extraction is the process of identifying and returning the values associated with a ‘target’ raster at specific locations, based on a (typically vector) geographic ‘selector’ object.
The results depend on the type of selector used (points, lines or polygons) and arguments passed to the terra::extract() function.
The reverse of raster extraction — assigning raster cell values based on vector objects — is rasterization, described in Section 6.4.
The basic example is of extracting the value of a raster cell at specific points.
For this purpose, we will use zion_points, which contain a sample of 30 locations within Zion National Park (Figure 6.2).
The following command extracts elevation values from srtm and creates a data frame with points’ IDs (one value per vector’s row) and related srtm values for each point.
Now, we can add the resulting object to our zion_points dataset with the cbind() function:
data("zion_points", package = "spDataLarge")
elevation = terra::extract(srtm, zion_points)
zion_points = cbind(zion_points, elevation)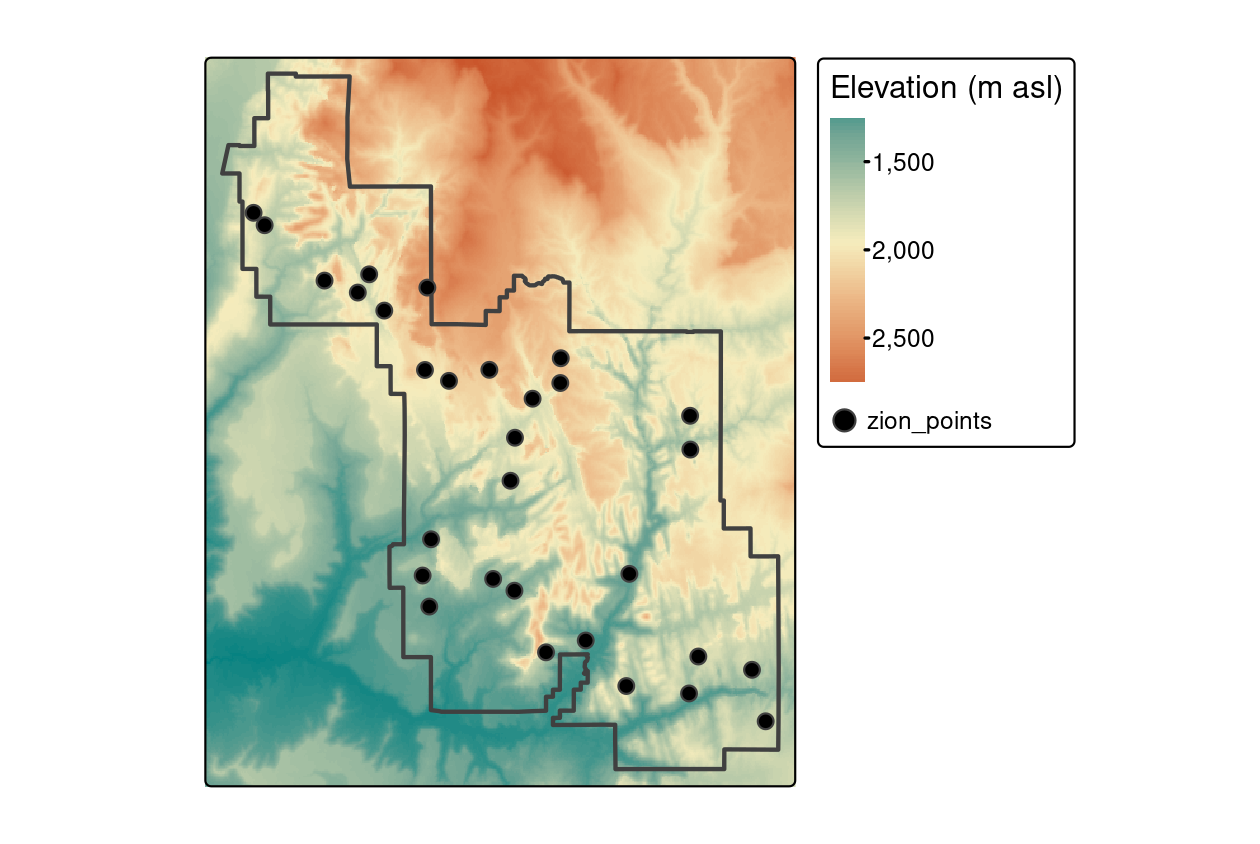
FIGURE 6.2: Locations of points used for raster extraction.
Raster extraction also works with line selectors. Then, it extracts one value for each raster cell touched by a line. However, the line extraction approach is not recommended to obtain values along the transects, as it is hard to get the correct distance between each pair of extracted raster values.
In this case, a better approach is to split the line into many points and then extract the values for these points.
To demonstrate this, the code below creates zion_transect, a straight line going from northwest to southeast of Zion National Park, illustrated in Figure 6.3(A) (see Section 2.2 for a recap on the vector data model):
zion_transect = cbind(c(-113.2, -112.9), c(37.45, 37.2)) |>
st_linestring() |>
st_sfc(crs = crs(srtm)) |>
st_sf(geometry = _)The utility of extracting heights from a linear selector is illustrated by imagining that you are planning a hike. The method demonstrated below provides an ‘elevation profile’ of the route (the line does not need to be straight), useful for estimating how long it will take due to long climbs.
The first step is to add a unique id for each transect.
Next, with the st_segmentize() function we can add points along our line(s) with a provided density (dfMaxLength) and convert them into points with st_cast().
zion_transect$id = 1:nrow(zion_transect)
zion_transect = st_segmentize(zion_transect, dfMaxLength = 250)
zion_transect = st_cast(zion_transect, "POINT")Now, we have a large set of points, and we want to derive a distance between the first point in our transects and each of the subsequent points. In this case, we only have one transect, but the code, in principle, should work on any number of transects:
zion_transect = zion_transect |>
group_by(id) |>
mutate(dist = st_distance(geometry)[, 1]) Finally, we can extract elevation values for each point in our transects and combine this information with our main object.
The resulting zion_transect can be used to create elevation profiles, as illustrated in Figure 6.3(B).
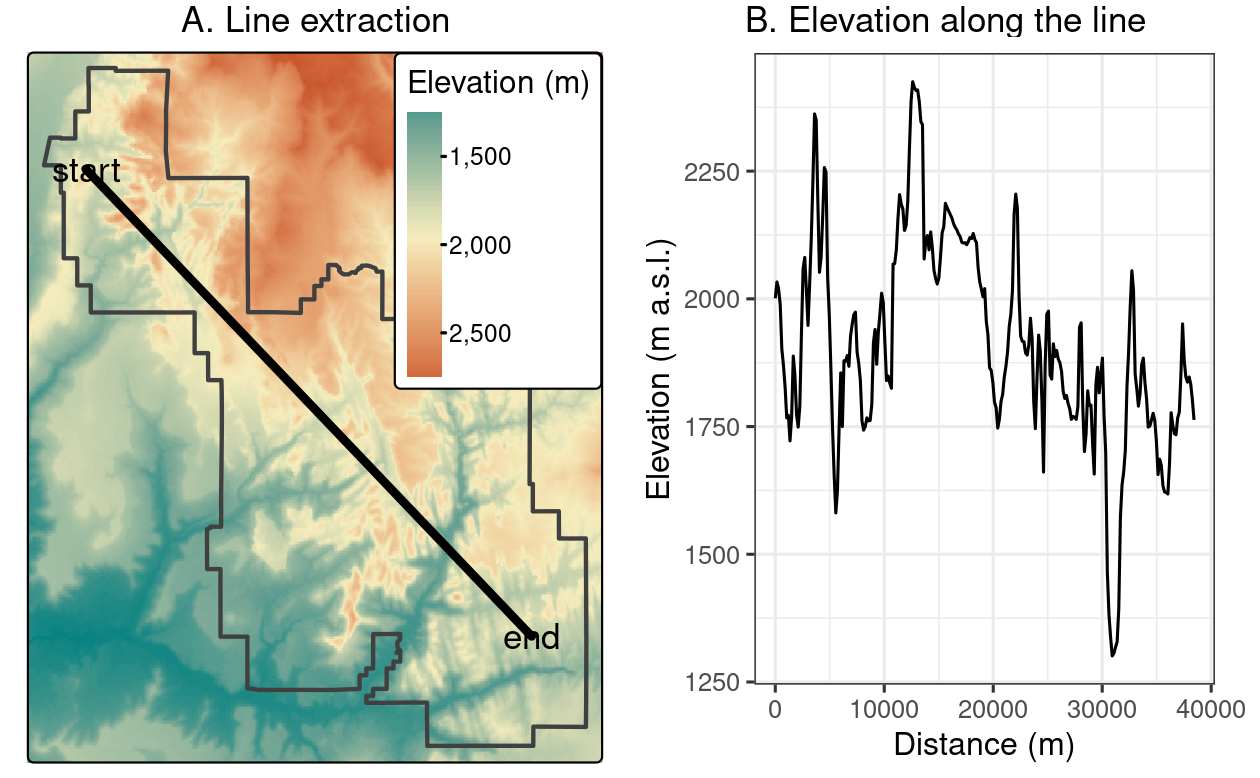
FIGURE 6.3: Location of a line used for (A) raster extraction and (B) the elevation along this line.
The final type of geographic vector object for raster extraction is polygons.
Like lines, polygons tend to return many raster values per polygon.
This is demonstrated in the command below, which results in a data frame with column names ID (the row number of the polygon) and srtm (associated elevation values):
zion_srtm_values = terra::extract(x = srtm, y = zion)Such results can be used to generate summary statistics for raster values per polygon, for example to characterize a single region or to compare many regions.
This is shown in the code below, which creates the object zion_srtm_df containing summary statistics for elevation values in Zion National Park (see Figure 6.4(A)):
group_by(zion_srtm_values, ID) |>
summarize(across(srtm, list(min = min, mean = mean, max = max)))
#> # A tibble: 1 × 4
#> ID srtm_min srtm_mean srtm_max
#> <dbl> <int> <dbl> <int>
#> 1 1 1122 1818. 2661The preceding code chunk used dplyr to provide summary statistics for cell values per polygon ID, as described in Chapter 3. The results provide useful summaries, for example that the maximum height in the park is around 2,661 meters above sea level (other summary statistics, such as standard deviation, can also be calculated in this way). Because there is only one polygon in the example, a data frame with a single row is returned; however, the method works when multiple selector polygons are used.
A similar approach works for counting occurrences of categorical raster values within polygons.
This is illustrated with a land cover dataset (nlcd) from the spDataLarge package in Figure 6.4(B), and demonstrated in the code below:
nlcd = rast(system.file("raster/nlcd.tif", package = "spDataLarge"))
zion2 = st_transform(zion, st_crs(nlcd))
zion_nlcd = terra::extract(nlcd, zion2)
zion_nlcd |>
group_by(ID, levels) |>
count()
#> # A tibble: 7 × 3
#> # Groups: ID, levels [7]
#> ID levels n
#> <dbl> <fct> <int>
#> 1 1 Developed 4205
#> 2 1 Barren 98285
#> 3 1 Forest 298299
#> 4 1 Shrubland 203701
#> # ℹ 3 more rows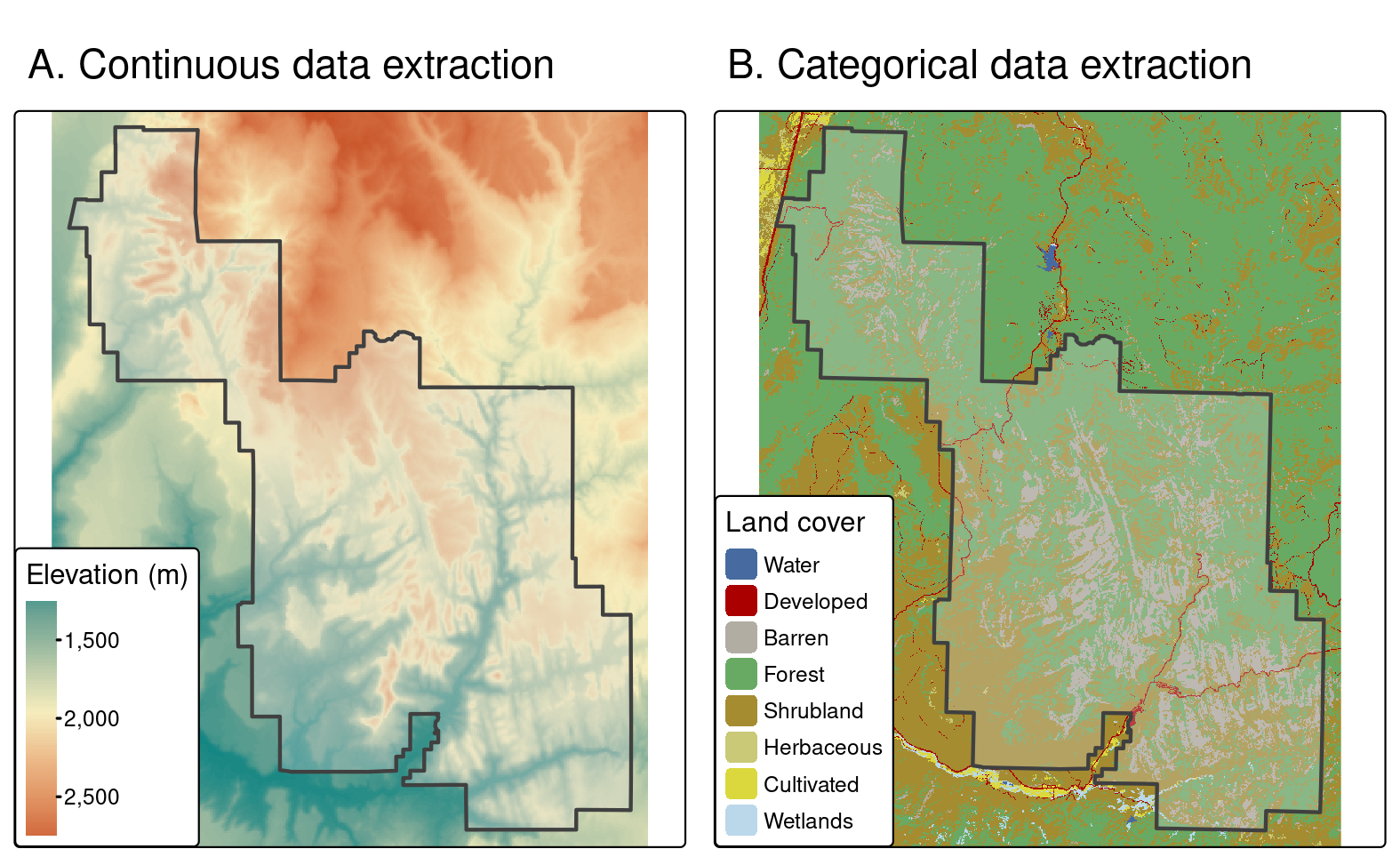
FIGURE 6.4: Area used for (A) continuous and (B) categorical raster extraction.
Although the terra package offers rapid extraction of raster values within polygons, extract() can still be a bottleneck when processing large polygon datasets.
The exactextractr package offers a significantly faster alternative for extracting pixel values through the exact_extract() function.
The exact_extract() function also computes, by default, the fraction of each raster cell overlapped by the polygon, which is more precise (see note below for details).
terra::extract() function has an argument called exact.
With exact = TRUE, we get one more column fraction in the output data frame, which represents a fraction of each cell that is covered by the polygon.
This could be useful to calculate, for example, a weighted mean for continuous rasters or more precise coverage for categorical rasters.
By default, it is FALSE, as this operation requires more computations.
The exactextractr::exact_extract() function always computes the coverage fraction of the polygon in each cell.
6.4 Rasterization
Rasterization is the conversion of vector objects into their representation in raster objects. Usually, the output raster is then used for quantitative analysis (e.g., analysis of terrain) or modeling. As we saw in Chapter 2, the raster data model has some characteristics that make it conducive to certain methods. Furthermore, the process of rasterization can help simplify datasets because the resulting values all have the same spatial resolution: rasterization can be seen as a special type of geographic data aggregation.
The terra package contains the function rasterize() for doing this work.
Its first two arguments are, x, vector object to be rasterized and, y, a ‘template raster’ object defining the extent, resolution and CRS of the output.
The geographic resolution of the input raster has a major impact on the results: if it is too low (cell size is too large), the result may miss the full geographic variability of the vector data; if it is too high, computational times may be excessive.
There are no simple rules to follow when deciding an appropriate geographic resolution, which is heavily dependent on the intended use of the results.
Often the target resolution is imposed on the user, for example when the output of rasterization needs to be aligned to some other existing raster.
To demonstrate rasterization in action, we will use a template raster that has the same extent and CRS as the input vector data cycle_hire_osm_projected (a dataset on cycle hire points in London is illustrated in Figure 6.5(A)) and spatial resolution of 1000 meters:
cycle_hire_osm = spData::cycle_hire_osm
cycle_hire_osm_projected = st_transform(cycle_hire_osm, "EPSG:27700")
raster_template = rast(ext(cycle_hire_osm_projected), resolution = 1000,
crs = crs(cycle_hire_osm_projected))Rasterization is a very flexible operation: the results depend not only on the nature of the template raster, but also on the type of input vector (e.g., points, polygons) and a variety of arguments taken by the rasterize() function.
To illustrate this flexibility, we will try three different approaches to rasterization.
First, we create a raster representing the presence or absence of cycle hire points (known as presence/absence rasters).
In this case rasterize() requires no argument in addition to x and y, the aforementioned vector and raster objects (results illustrated Figure 6.5(B)).
ch_raster1 = rasterize(cycle_hire_osm_projected, raster_template)The fun argument specifies summary statistics used to convert multiple observations in close proximity into associate cells in the raster object.
By default fun = "last" is used, but other options such as fun = "length" can be used, in this case to count the number of cycle hire points in each grid cell (the results of this operation are illustrated in Figure 6.5(C)).
ch_raster2 = rasterize(cycle_hire_osm_projected, raster_template,
fun = "length")The new output, ch_raster2, shows the number of cycle hire points in each grid cell.
The cycle hire locations have different numbers of bicycles described by the capacity variable, raising the question, what’s the capacity in each grid cell?
To calculate that we must sum the field ("capacity"), resulting in output illustrated in Figure 6.5(D), calculated with the following command (other summary functions such as mean could be used).
ch_raster3 = rasterize(cycle_hire_osm_projected, raster_template,
field = "capacity", fun = sum, na.rm = TRUE)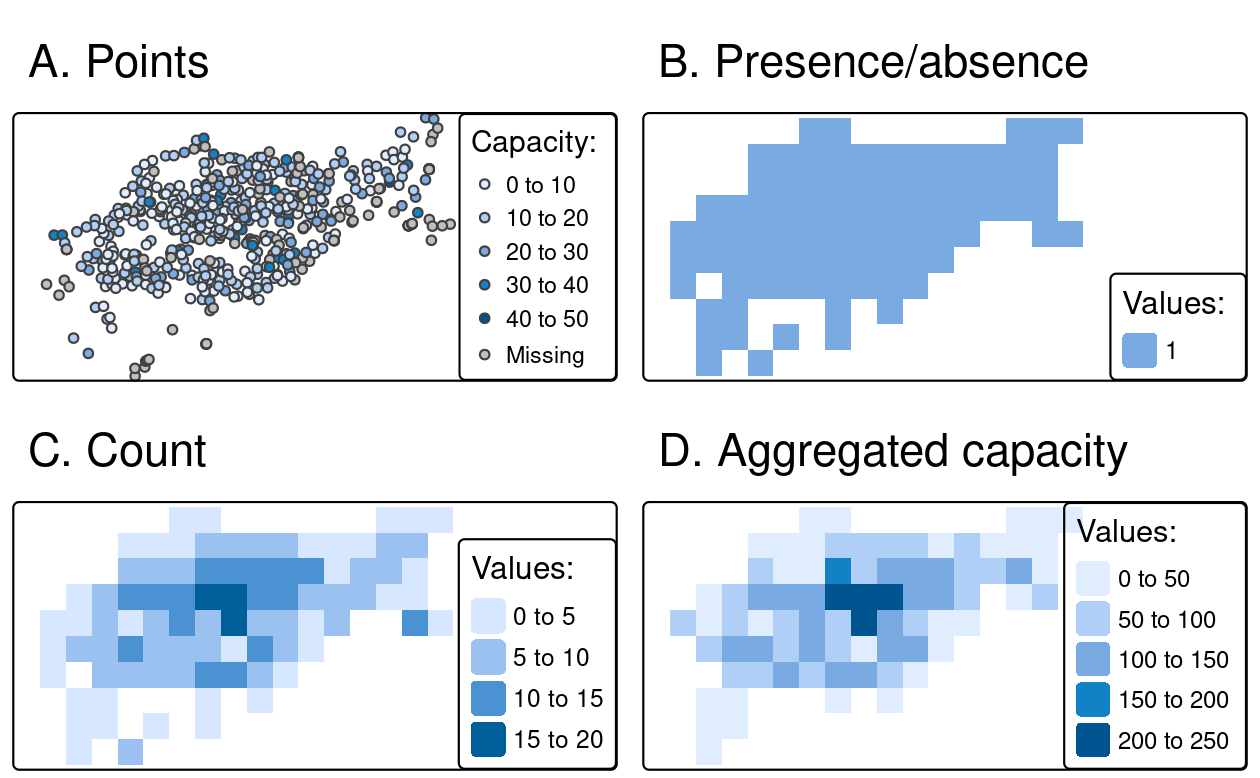
FIGURE 6.5: Examples of point rasterization.
Another dataset based on California’s polygons and borders (created below) illustrates rasterization of lines. After casting the polygon objects into a multilinestring, a template raster is created with a resolution of a 0.5 degree:
california = dplyr::filter(us_states, NAME == "California")
california_borders = st_cast(california, "MULTILINESTRING")
raster_template2 = rast(ext(california), resolution = 0.5,
crs = st_crs(california)$wkt)When considering line or polygon rasterization, one useful additional argument is touches.
By default it is FALSE, but when changed to TRUE, all cells that are touched by a line or polygon border get a value.
Line rasterization with touches = TRUE is demonstrated in the code below (Figure 6.6(A)).
california_raster1 = rasterize(california_borders, raster_template2,
touches = TRUE)Compare it to a polygon rasterization, with touches = FALSE by default, which selects only raster cells whose centroids are inside the selector polygon, as illustrated in Figure 6.6(B).
california_raster2 = rasterize(california, raster_template2) 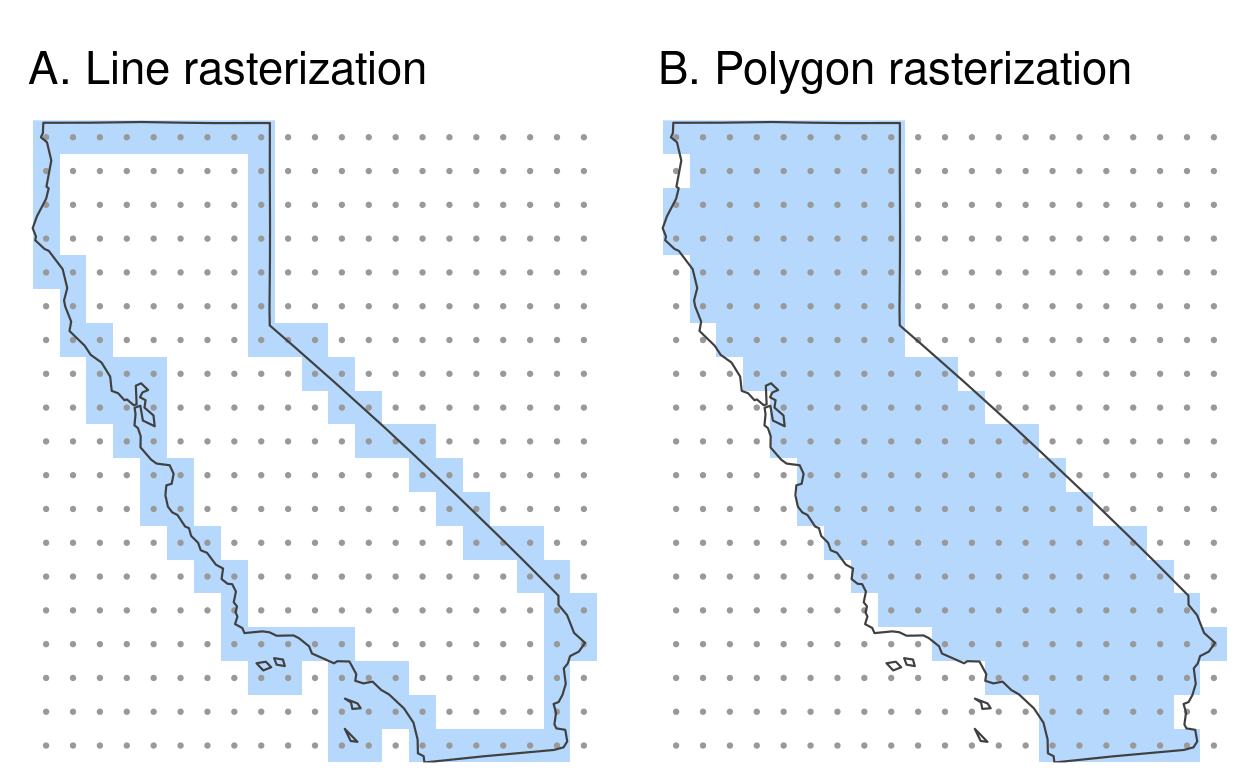
FIGURE 6.6: Examples of line and polygon rasterizations.
6.5 Spatial vectorization
Spatial vectorization is the counterpart of rasterization (Section 6.4), but in the opposite direction. It involves converting spatially continuous raster data into spatially discrete vector data such as points, lines or polygons.
for-loops and alike by doing things like 1:10 / 2 (see also Wickham (2019)).
The simplest form of vectorization is to convert the centroids of raster cells into points.
as.points() does exactly this for all non-NA raster grid cells (Figure 6.7).
Note, here we also used st_as_sf() to convert the resulting object to the sf class.
elev = rast(system.file("raster/elev.tif", package = "spData"))
elev_point = as.points(elev) |>
st_as_sf()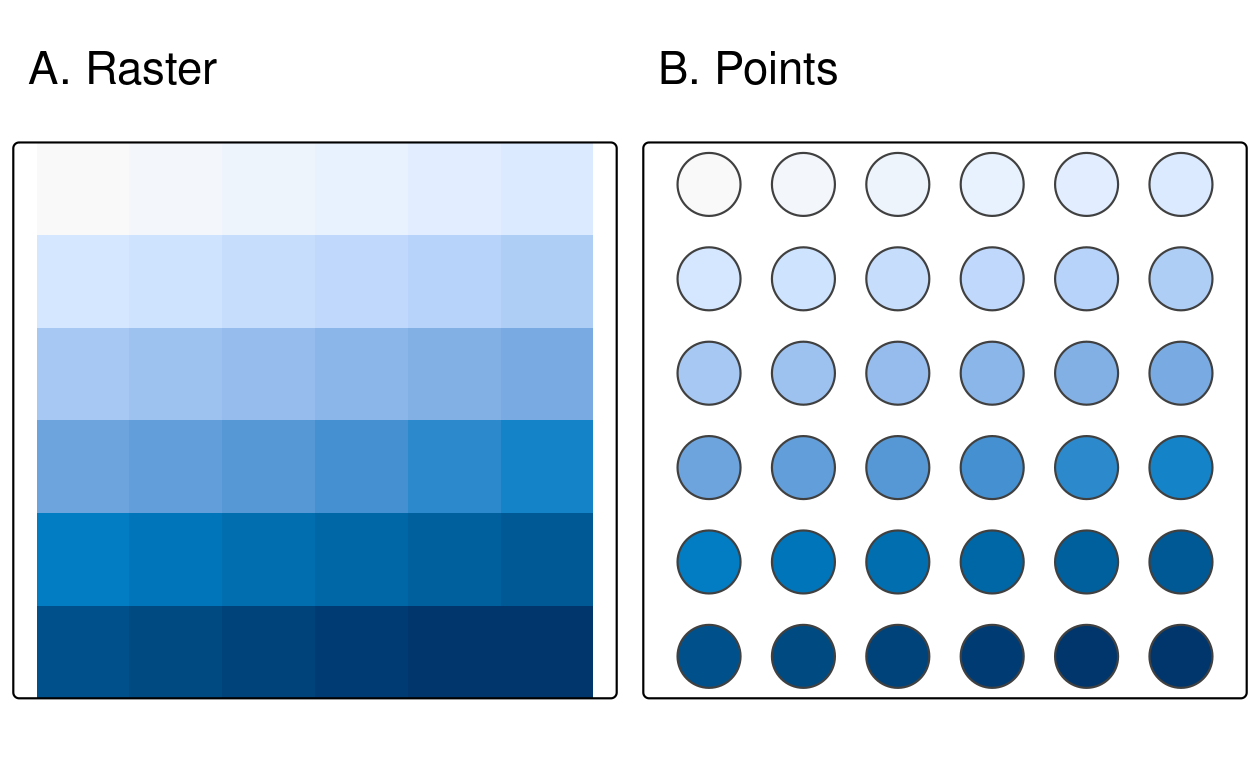
FIGURE 6.7: Raster and point representation of the elev object.
Another common type of spatial vectorization is the creation of contour lines representing lines of continuous height or temperatures (isotherms), for example.
We will use a real-world digital elevation model (DEM) because the artificial raster elev produces parallel lines (task for the reader: verify this and explain why this happens).
Contour lines can be created with the terra function as.contour(), which is itself a wrapper around the built-in R function filled.contour(), as demonstrated below (not shown):
dem = rast(system.file("raster/dem.tif", package = "spDataLarge"))
cl = as.contour(dem) |>
st_as_sf()
plot(dem, axes = FALSE)
plot(cl, add = TRUE)Contours can also be added to existing plots with functions such as contour(), rasterVis::contourplot().
As illustrated in Figure 6.8, isolines can be labeled.
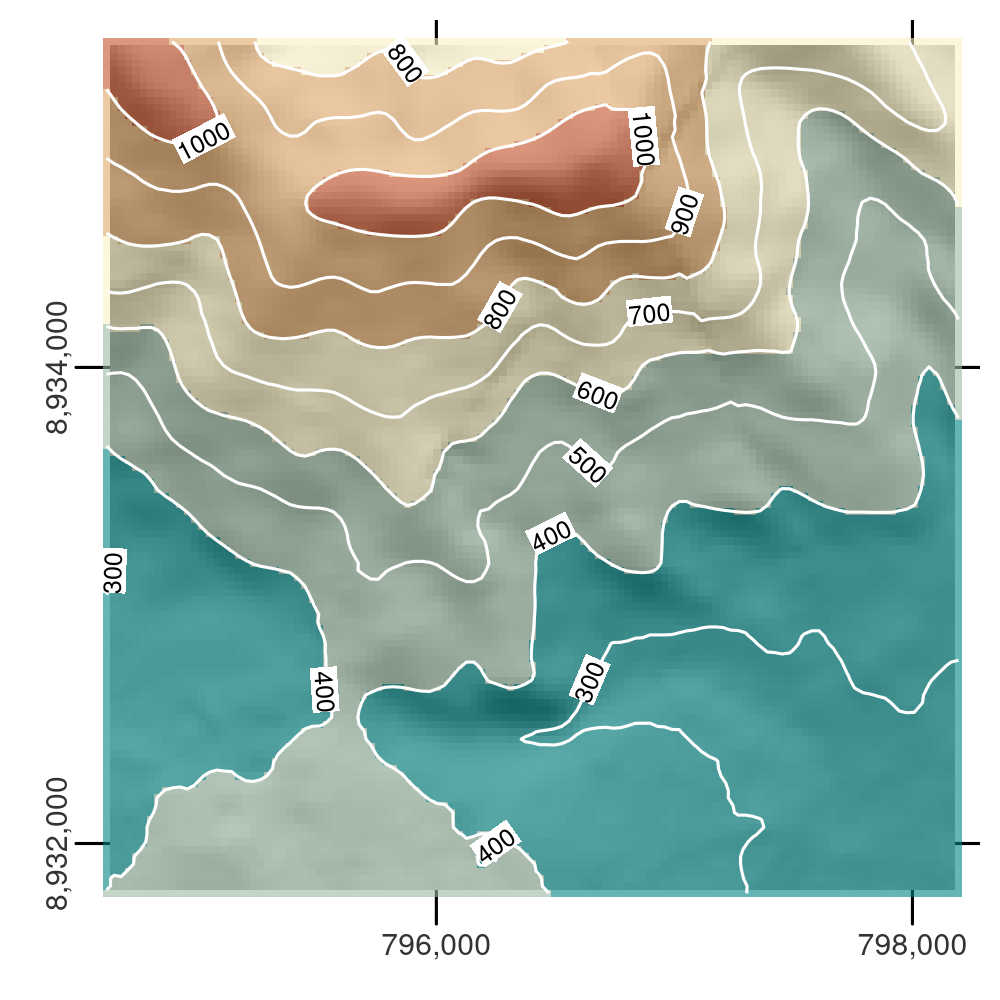
FIGURE 6.8: Digital elevation model with hillshading, showing the southern flank of Mt. Mongón overlaid with contour lines.
The final type of vectorization involves conversion of rasters to polygons.
This can be done with terra::as.polygons(), which converts each raster cell into a polygon consisting of five coordinates, all of which are stored in memory (explaining why rasters are often fast compared with vectors!).
This is illustrated below by converting the grain object into polygons and subsequently dissolving borders between polygons with the same attribute values (also see the dissolve argument in as.polygons()).
grain = rast(system.file("raster/grain.tif", package = "spData"))
grain_poly = as.polygons(grain) |>
st_as_sf()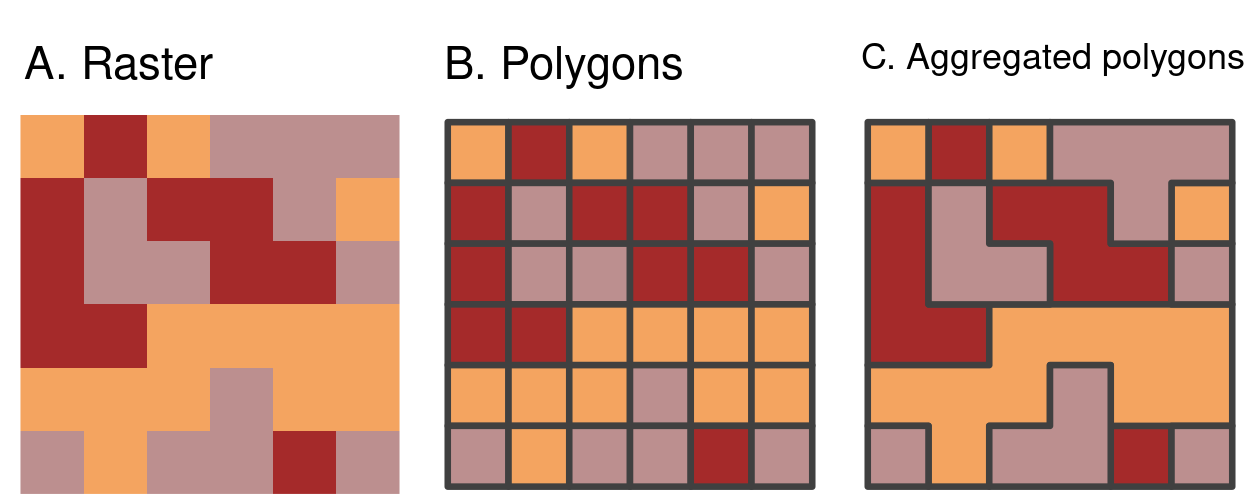
FIGURE 6.9: Vectorization of (A) raster into (B) polygons (dissolve = FALSE) and aggregated polygons (dissolve = TRUE).
The aggregated polygons of the grain dataset have rectilinear boundaries which arise from being defined by connecting rectangular pixels.
The smoothr package described in Chapter 5 can be used to smooth the edges of the polygons.
As smoothing removes sharp edges in the polygon boundaries, the smoothed polygons will not have the same exact spatial coverage as the original pixels.
Caution should therefore be taken when using the smoothed polygons for further analysis.
6.6 Exercises
Some of the following exercises use a vector (zion_points) and raster dataset (srtm) from the spDataLarge package.
They also use a polygonal ‘convex hull’ derived from the vector dataset (ch) to represent the area of interest:
library(sf)
library(terra)
library(spData)
zion_points_path = system.file("vector/zion_points.gpkg", package = "spDataLarge")
zion_points = read_sf(zion_points_path)
srtm = rast(system.file("raster/srtm.tif", package = "spDataLarge"))
ch = st_combine(zion_points) |>
st_convex_hull() |>
st_as_sf()E1. Crop the srtm raster using (1) the zion_points dataset and (2) the ch dataset.
Are there any differences in the output maps?
Next, mask srtm using these two datasets.
Can you see any difference now?
How can you explain that?
E2. Firstly, extract values from srtm at the points represented in zion_points.
Next, extract average values of srtm using a 90 buffer around each point from zion_points and compare these two sets of values.
When would extracting values by buffers be more suitable than by points alone?
- Bonus: Implement extraction using the exactextractr package and compare the results.
E3. Subset points higher than 3100 meters in New Zealand (the nz_height object) and create a template raster with a resolution of 3 km for the extent of the new point dataset.
Using these two new objects:
- Count numbers of the highest points in each grid cell.
- Find the maximum elevation in each grid cell.
E4. Aggregate the raster counting high points in New Zealand (created in the previous exercise), reduce its geographic resolution by half (so cells are 6 x 6 km) and plot the result.
- Resample the lower resolution raster back to the original resolution of 3 km. How have the results changed?
- Name two advantages and disadvantages of reducing raster resolution.
E5. Polygonize the grain dataset and filter all squares representing clay.
- Name two advantages and disadvantages of vector data over raster data.
- When would it be useful to convert rasters to vectors in your work?