7 Reprojeté des données geographiques

Prérequis

• Ce chapitre nécessite les paquets suivants :

library(sf)
library(terra)
library(dplyr)
library(spData)
library(spDataLarge)

7.1 Introduction

La section 2.4 a présenté les coordonnées dans un système de référence (CRS), en mettant l’accent sur les deux principaux types : Les systèmes de coordonnées géographiques (‘lon/lat’, avec des unités en degrés de longitude et de latitude) et projetés (généralement avec des unités de mètres à partir d’un datum). Ce chapitre pat de ces connaissances et va plus loin. Il montre comment définir et transformer des données géographiques d’un CRS à un autre et, en outre, il met en évidence les problèmes spécifiques qui peuvent survenir en raison de l’ignorance des CRS et dont vous devez être conscient, en particulier si vos données sont stockées avec des coordonnées longitude/latitude.

Dans de nombreux projets, il n’est pas nécessaire de se préoccuper des différents CRS, et encore moins de les convertir. Il est important de savoir si vos données sont dans un système de coordonnées projeté ou géographique, et les conséquences pour les opérations sur les géométries. Toutefois, si vous connaissez le CRS de vos données et êtes conscient des effets de ces choix (abordées dans la section suivante), les CRS devraient marcher sans effort en coulisses. Cependant quand les choses tournent mal il devient important d’en savoir plus. Le fait de disposer d’un CRS de projet clairement défini dans lequel se trouvent toutes les données du projet, et de comprendre comment et pourquoi utiliser différents CRS, permet heureusement d’éviter des situations difficiles. En outre, l’apprentissage des systèmes de coordonnées approfondira votre connaissance des jeux de données géographiques et permettra de les utiliser plus efficacement.

Ce chapitre présente les principes fondamentaux des CRS, les conséquences de l’utilisation de différents CRS (y compris ce qui peut mal tourner) et la manière de “reprojeter” des jeux de données d’un système de coordonnées à un autre. La section suivante présente les CRS dans R, suivie de la section 7.2 qui montre comment obtenir et définir les CRS associés aux objets spatiaux. La section 7.4 démontre l’importance de savoir dans quel CRS se trouvent vos données en se référant à un exemple de création de tampons (buffer). Nous abordons les questions de savoir quand reprojeter et quel CRS utiliser dans la section 7.5 puis la section 7.6. Nous couvrons la reprojection des objets vectoriels et des rasters dans les sections 7.7 et 7.8 et la modification des projections [TODO a corriger] cartographiques dans la section 7.9.

7.2 coordonnées dans un système de référence

La plupart des outils géographiques modernes nécessitant des conversions CRS, y compris les principaux paquets R-spatial et les logiciels SIG de bureau tels que QGIS, s’interfacent avec PROJ, une bibliothèque C++ open source qui “transforme les coordonnées d’un système de référence de coordonnées (CRS) en un autre”. Les CRS peuvent être décrits de nombreuses façons, notamment les suivantes.

1. Des déclarations simples mais potentiellement ambiguës telles que “c’est en coordonnées lon/lat”.
2. Des “une ligne de caractères proj4 (proj4 strings)” formalisées mais maintenant dépassées, telles que +proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs.
3. Avec une chaîne de caractères d’identification “authority:code” telle que EPSG:4326.

Tous font référence à la même chose : le système de coordonnées “WGS84” qui constitue la base des coordonnées du système de positionnement global (GPS) et de nombreux autres jeux de données. Mais lequel est correct ??

La réponse courte est que la troisième façon d’identifier les CRS est correcte : EPSG:4326 est compris par les paquets sf (et par extension stars) et terra couverts dans ce livre, ainsi que par de nombreux autres projets logiciels pour travailler avec des données géographiques, comme [QGIS] (https://docs.qgis.org/3.16/en/docs/user_manual/working_with_projections/working_with_projections.html) et [PROJ] (https://proj.org/development/quickstart.html). EPSG:4326 est à l’épreuve du temps. En outre, bien qu’il soit lisible par une machine, contrairement à la représentation par une ligne de caractères (proj-sring), “EPSG:4326” est court, facile à retenir et très facile à trouver en ligne (une recherche sur EPSG:4326 donne une page dédiée sur le site epsg.io, par exemple). L’identifiant plus concis 4326 est compris par sf, mais nous recommandons la représentation plus explicite AUTHORITY:CODE pour éviter toute ambiguïté et fournir un contexte.

La réponse la plus longue est qu’aucune des trois descriptions n’est suffisante et que davantage de détails sont nécessaires pour une manipulation et des transformations non ambiguës des CRS : en raison de la complexité de ces derniers, il n’est pas possible de capturer toutes les informations pertinentes les concernant dans des chaînes de caractères aussi courtes. Pour cette raison, l’Open Geospatial Consortium (OGC, qui a également développé la spécification des fonctionnalités simples que le paquet sf met en œuvre) a développé un format standard ouvert pour décrire les CRS, appelé WKT (Well Known Text). Ce format est détaillé dans un [document de plus de 100 pages] (https://portal.opengeospatial.org/files/18-010r7) qui “définit la structure et le contenu d’une mise en œuvre de chaîne de caractères du modèle abstrait de systèmes de référence de coordonnées décrit dans la norme ISO 19111:2019” (Open Geospatial Consortium 2019). La représentation WKT du SRC WGS84, qui a l’identifiant EPSG:4326 est la suivante :

st_crs("EPSG:4326")
#> Coordinate Reference System:
#>   User input: EPSG:4326 
#>   wkt:
#> GEOGCRS["WGS 84",
#>     ENSEMBLE["World Geodetic System 1984 ensemble",
#>         MEMBER["World Geodetic System 1984 (Transit)"],
#>         MEMBER["World Geodetic System 1984 (G730)"],
#>         MEMBER["World Geodetic System 1984 (G873)"],
#>         MEMBER["World Geodetic System 1984 (G1150)"],
#>         MEMBER["World Geodetic System 1984 (G1674)"],
#>         MEMBER["World Geodetic System 1984 (G1762)"],
#>         MEMBER["World Geodetic System 1984 (G2139)"],
#>         ELLIPSOID["WGS 84",6378137,298.257223563,
#>             LENGTHUNIT["metre",1]],
#>         ENSEMBLEACCURACY[2.0]],
#>     PRIMEM["Greenwich",0,
#>         ANGLEUNIT["degree",0.0174532925199433]],
#>     CS[ellipsoidal,2],
#>         AXIS["geodetic latitude (Lat)",north,
#>             ORDER[1],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         AXIS["geodetic longitude (Lon)",east,
#>             ORDER[2],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>     USAGE[
#>         SCOPE["Horizontal component of 3D system."],
#>         AREA["World."],
#>         BBOX[-90,-180,90,180]],
#>     ID["EPSG",4326]]

La sortie de la commande montre comment l’identifiant du CRS (également connu sous le nom d’identifiant de référence spatiale ou SRID) fonctionne : il s’agit simplement d’une liste fournissant un identifiant unique associé à une représentation WKT plus complète du CRS. Cela soulève la question suivante : que se passe-t-il s’il y a un décalage entre l’identifiant et la représentation WKT plus longue? Sur ce point, Open Geospatial Consortium (2019) est clair : la représentation WKT détaillée a la priorité sur l’identifiant :

Should any attributes or values given in the cited identifier be in conflict with attributes or values given explicitly in the WKT description, the WKT values shall prevail.

La convention consistant à se référer aux identifiants des CRS sous la forme AUTHORITY:CODE, qui est également utilisée par les logiciels géographiques écrits dans d’autres langages, permet de se référer à un large éventail de systèmes de coordonnées formellement définis.²⁶ L’autorité la plus couramment utilisée dans les identificateurs de CRS est EPSG, un acronyme de l’European Petroleum Survey Group qui a publié une liste normalisée de CRS (l’EPSG a été repris par l’organisme pétrolier et gazier Geomatics Committee of the International Association of Oil & Gas Producers en 2005). D’autres autorités peuvent être utilisées dans les identifiants CRS. ESRI:54030, par exemple, fait référence à la mise en œuvre de la projection Robinson par ESRI, qui a la chaîne WKT suivante (seules les 8 premières lignes sont affichées) :

sf::st_crs("ESRI:54030")
#> Coordinate Reference System:
#>   User input: ESRI:54030 
#>   wkt:
#> PROJCRS["World_Robinson",
#>     BASEGEOGCRS["WGS 84",
#>         DATUM["World Geodetic System 1984",
#>             ELLIPSOID["WGS 84",6378137,298.257223563,
#>                 LENGTHUNIT["metre",1]]],
#> ...

Les chaînes de caractères WKT sont exhaustives, détaillées et précises, ce qui permet de stocker et de transformer les CRS sans ambiguïté. Elles contiennent toutes les informations pertinentes sur un CRS donné, y compris son datum et son ellipsoïde, son méridien d’origine, sa projection et ses unités.²⁷

Les versions récentes de PROJ (6+) permettent toujours l’utilisation de proj-strings pour définir des opérations de coordonnées, mais certaines clés de proj-string (+nadgrids, +towgs84, +k, +init=epsg:) ne sont plus supportées ou sont déconseillées. De plus, seuls trois systèmes de référence (WGS84, NAD83 et NAD27) peuvent être directement définis dans desproj-string. De plus longues explications sur l’évolution des définitions CRS et de la bibliothèque PROJ peuvent être trouvées dans Bivand (2021), le chapitre 2 de Pebesma and Bivand (2022), et le billet de blog de Floris Vanderhaeghe Comme indiqué dans la documentation PROJ, il existe différentes versions du format WKT CRS, notamment WKT1 et deux variantes de WKT2, dont la dernière (WKT2, spécification 2018) correspond à la norme ISO 19111:2019 (Open Geospatial Consortium 2019).

7.3 Interrogation et réglage des systèmes de coordonnées

Voyons comment les CRS sont stockés dans les objets spatiaux de R et comment ils peuvent être interrogés et définis. Tout d’abord, nous allons voir comment obtenir et définir les CRS dans les objets de données géographiques vectoriels, en commençant par l’exemple suivant :

vector_filepath = system.file("shapes/world.gpkg", package = "spData")
new_vector = read_sf(vector_filepath)

Notre nouvel objet, new_vector, est un tableau de données de classe sf qui représente les pays du monde entier (voir la page d’aide ?spData::world pour plus de détails). Le CRS peut être récupéré avec la fonction sf st_crs().

st_crs(new_vector) # obtenir le CRS
#> Coordinate Reference System:
#>   User input: WGS 84 
#>   wkt:
#>   ...

La sortie est une liste contenant deux composants principaux :

1. USer input (dans ce cas WGS 84, un synonyme de EPSG:4326 qui dans ce cas a été pris du fichier en entrée), correspondant aux identifiants CRS décrits ci-dessus
2. wkt, contenant la chaîne WKT complète avec toutes les informations pertinentes sur le CRS.

L’élément input est flexible, et selon le fichier d’entrée ou l’entrée fourni par l’utilisateur, il peut contenir la représentation AUTHORITY:CODE (par exemple, EPSG:4326), le nom du CRS (par exemple, WGS 84), ou même la définition de la proj-string. L’élément wkt stocke la représentation WKT, qui est utilisée lors de la sauvegarde de l’objet dans un fichier ou lors d’opérations sur les coordonnées. Ci-dessus, nous pouvons voir que l’objet new_vector possède l’ellipsoïde WGS84, utilise le premier méridien de Greenwich, et l’ordre des axes est latitude et longitude. Dans ce cas, nous avons également quelques éléments supplémentaires, tels que USAGE expliquant la zone appropriée pour l’utilisation de ce CRS, et ID pointant sur l’identifiant du CRS : EPSG:4326.

La fonction st_crs possède également une fonctionnalité très utile : nous pouvons récupérer des informations supplémentaires sur le CRS utilisé. Par exemple, essayez d’exécuter :

• st_crs(new_vector)$IsGeographic pour vérifier si le CRS est géographique ou non
• st_crs(new_vector)$units_gdal pour connaître les unités du CRS
• st_crs(new_vector)$srid extrait son identifiant “SRID” (lorsqu’il est disponible)
• st_crs(new_vector)$proj4string extrait la représentation de la chaîne de projet.

Dans les cas où un système de référence de coordonnées (CRS) est manquant ou le mauvais CRS est défini, la fonction st_set_crs() peut être utilisée (dans ce cas, la chaîne WKT reste inchangée car le CRS était déjà défini correctement lors de la lecture du fichier) :

new_vector = st_set_crs(new_vector, "EPSG:4326") # set CRS

L’obtention et le paramétrage des CRS fonctionnent de manière similaire pour les objets de données géographiques raster. La fonction crs() du paquet terra accède aux informations CRS d’un objet SpatRaster (notez l’utilisation de la fonction cat() pour les imprimer joliment) :

raster_filepath = system.file("raster/srtm.tif", package = "spDataLarge")
my_rast = rast(raster_filepath)
cat(crs(my_rast)) # obtenir le CRS
#> GEOGCRS["WGS 84",
#>     DATUM["World Geodetic System 1984",
#>         ELLIPSOID["WGS 84",6378137,298.257223563,
#>             LENGTHUNIT["metre",1]]],
#>     PRIMEM["Greenwich",0,
#>         ANGLEUNIT["degree",0.0174532925199433]],
#>     CS[ellipsoidal,2],
#>         AXIS["geodetic latitude (Lat)",north,
#>             ORDER[1],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         AXIS["geodetic longitude (Lon)",east,
#>             ORDER[2],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>     ID["EPSG",4326]]

La sortie est la représentation standard en WKT du CRS. La même fonction, crs(), peut également être utilisée pour définir un CRS pour les objets raster.

crs(my_rast) = "EPSG:26912" # définir le CRS

Ici, nous pouvons utiliser soit l’identifiant (recommandé dans la plupart des cas) ou la représentation WKT complète. Des méthodes alternatives pour définir les crs incluent les chaînes de caractères proj-string ou les CRS extraits à partir d’autres objets existants avec crs(). Ces approches peuvent être moins pérennes.

Il est important de noter que les fonctions st_crs() et crs() ne modifient pas les valeurs des coordonnées ou les géométries. Leur rôle est seulement de définir une information des métadonnées sur l’objet CRS.

Dans certains cas, le CRS d’un objet géographique est inconnu, comme c’est le cas dans le jeu de données london créé dans l’extrait de code ci-dessous, à partir de l’exemple de Londres introduit dans la section ?? :

london = data.frame(lon = -0.1, lat = 51.5) |> 
  st_as_sf(coords = c("lon", "lat"))
st_is_longlat(london)
#> [1] NA

La sortie NA montre que sf ne sait pas quel est le CRS et ne veut pas le deviner (NA signifie littéralement ‘non disponible’). A moins qu’un CRS soit spécifié manuellement ou soit chargé à partir d’une source qui possède des métadonnées CRS, sf ne fait aucune hypothèse explicite sur les systèmes de coordonnées, autre que de dire “je ne sais pas”. Ce comportement est logique étant donné la diversité des CRS disponibles, mais diffère de certaines approches, comme la spécification du format de fichier GeoJSON, qui fait l’hypothèse simplificatrice que toutes les coordonnées ont un CRS lon/lat : EPSG:4326.

Un CRS peut être ajouté aux objets sf de trois manières principales :

• En assignant le CRS à un objet préexistant, par exemple avec st_crs(london) = "EPSG:4326".
• En passant un CRS à l’argument crs dans les fonctions sf qui créent des objets géométriques comme st_as_sf(... crs = "EPSG:4326"). Le même argument peut également être utilisé pour définir le CRS lors de la création de jeux de données rasters (par exemple, rast(crs = "EPSG:4326")).
• Avec la fonction st_set_crs(), qui retourne une version des données avec le nouveau CRS, une approche qui est démontrée dans le code suivant

london_geo = st_set_crs(london, "EPSG:4326")
st_is_longlat(london_geo)
#> [1] TRUE

Les jeux de données sans CRS spécifié peuvent poser des problèmes : toutes les coordonnées géographiques doivent avoir un système de coordonnées et le logiciel ne peut prendre de bonnes décisions concernant les opérations de traçage et de géométrie que s’il sait avec quel type de CRS il travaille.

7.4 Opérations géométriques sur des données projetées et non projetées

Depuis la version 1.0.0 de sf, la capacité de R à travailler avec des ensembles de données géographiques vectorielles comportant des CRS lon/lat a été considérablement améliorée, grâce à son intégration avec le moteur de géométrie sphérique S2 introduit dans la section 2.2.9. Comme le montre la figure 7.1, sf utilise soit GEOS, soit le S2 en fonction du type de CRS et de l’activation de S2 (il est activé par défaut). GEOS est toujours utilisé pour les données projetées et les données sans CRS ; pour les données géographiques, S2 est utilisé par défaut mais peut être désactivé avec sf::sf_use_s2(FALSE).

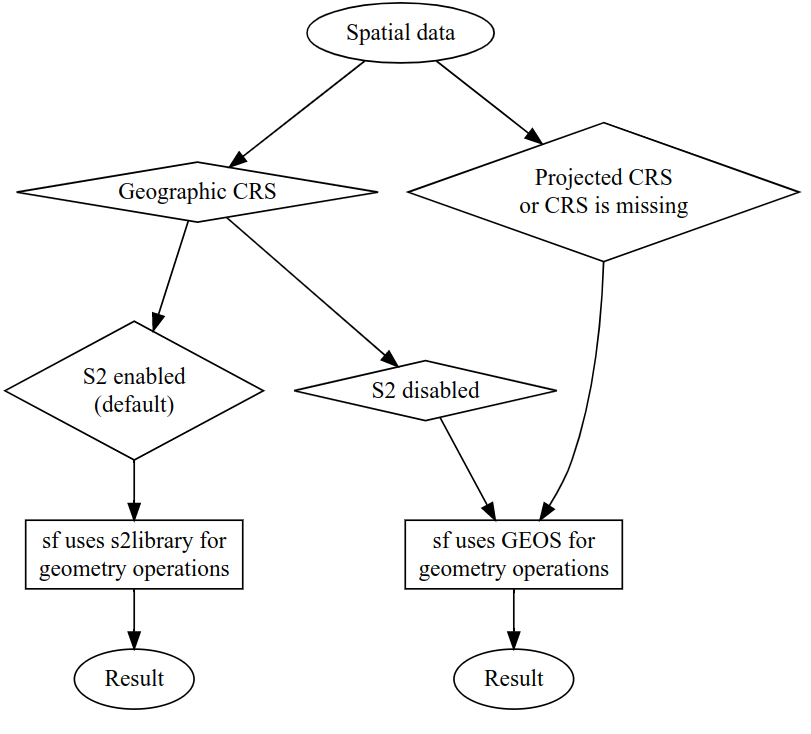
FIGURE 7.1: Comportement des opérations de géométrie dans le paquet sf en fonction du CRS des données d’entrée.

Pour démontrer l’importance des CRS, nous allons créer un tampon de 100 km autour de l’objet london de la section précédente. Nous allons également créer un tampon délibérément défectueux avec une “distance” de 1 degré, ce qui est à peu près équivalent à 100 km (1 degré est environ 111 km à l’équateur). Avant de plonger dans le code, il peut être utile de jeter un coup d’œil à la figure ?? pour avoir une idée des résultats que vous devriez être en mesure de reproduire en suivant les ligne de code ci-dessous.

La première étape consiste à créer trois tampons autour des objets london et london_geo créés ci-dessus avec des distances de 1 degré et 100 km (ou 100 000 m, ce qui peut être exprimé par 1e5 en notation scientifique) à partir du centre de Londres:

london_buff_no_crs = st_buffer(london, dist = 1)   # incorrect: pas de CRS
london_buff_s2 = st_buffer(london_geo, dist = 1e5) # utilisation de s2 par défaut
london_buff_s2_100_cells = st_buffer(london_geo, dist = 1e5, max_cells = 100) 

Dans la première ligne ci-dessus, sf suppose que l’entrée est projetée et génère un résultat qui a un tampon en unités de degrés, ce qui est problématique, comme nous allons le voir. Dans la deuxième ligne, sf utilise silencieusement le moteur de géométrie sphérique S2, introduit dans le chapitre 2, pour calculer l’étendue du tampon en utilisant la valeur par défaut de max_cells = 1000 — fixée à 100 dans la troisième ligne — avec les conséquences abordés plus loin (voir ?s2::s2_buffer_cells pour les détails). Pour mettre en évidence l’impact de l’utilisation par sf du moteur géométrique S2 pour les systèmes de coordonnées (géographiques) non projetés, nous allons le désactiver temporairement avec la commande sf_use_s2() (qui est activée, TRUE, par défaut), dans le morceau de code ci-dessous. Comme london_buff_no_crs, le nouvel objet london_geo est une abomination géographique : il a des unités de degrés, ce qui n’a aucun sens dans la grande majorité des cas :

sf::sf_use_s2(FALSE)
#> Spherical geometry (s2) switched off
london_buff_lonlat = st_buffer(london_geo, dist = 1) # résultat incorrect 
#> Warning in st_buffer.sfc(st_geometry(x), dist, nQuadSegs, endCapStyle =
#> endCapStyle, : st_buffer does not correctly buffer longitude/latitude data
#> dist is assumed to be in decimal degrees (arc_degrees).
sf::sf_use_s2(TRUE)
#> Spherical geometry (s2) switched on

Le message d’avertissement ci-dessus fait allusion à des problèmes liés à l’exécution d’opérations de géométrie planaire sur des données lon/lat. Lorsque les opérations de géométrie sphérique sont désactivées, avec la commande sf::sf_use_s2(FALSE), les tampons (et d’autres opérations géométriques) peuvent donner des résultats sans valeur car ils utilisent des unités de latitude et de longitude, un mauvais substitut pour les unités de distances appropriées telles que les mètres.

La distance entre deux lignes de longitude, appelées méridiens, est d’environ 111 km à l’équateur (exécutez geosphere::distGeo(c(0, 0), c(1, 0)) pour trouver la distance précise). Cette distance se réduit à zéro aux pôles. À la latitude de Londres, par exemple, les méridiens sont distants de moins de 70 km (défi : exécutez le code qui vérifie cela). Les lignes de latitude, en revanche, sont équidistantes les unes des autres quelle que soit la latitude : elles sont toujours distantes d’environ 111 km, y compris à l’équateur et près des pôles (voir les figures ?? à 7.4

N’interprétez pas l’avertissement concernant le CRS géographique (longitude/latitude) comme “le CRS ne devrait pas être défini” : il devrait presque toujours l’être! Il doit être mieux compris comme une suggestion de reprojeter les données sur un CRS projeté. Il n’est pas toujours nécessaire de tenir compte de cette suggestion : l’exécution d’opérations spatiales et géométriques fait peu ou pas de différence dans certains cas (par exemple, lors de sélection spatiale). Mais pour les opérations impliquant des distances, comme la mise en place de tampon, la seule façon de garantir un bon résultat (sans utiliser de moteurs de géométrie sphérique) est de créer une copie projetée des données et d’exécuter l’opération sur celle-ci. Les lignes de code ci-dessous indique comme le faire :

london_proj = data.frame(x = 530000, y = 180000) |> 
  st_as_sf(coords = 1:2, crs = "EPSG:27700")

Le résultat est un nouvel objet identique à london, mais reprojeté sur un CRS approprié (le British National Grid, ayant un code EPSG de 27700 dans ce cas) qui a des unités de mètres. Nous pouvons vérifier que le CRS a changé en utilisant st_crs() comme suit (une partie de la sortie a été remplacée par ...) :

st_crs(london_proj)
#> Coordinate Reference System:
#>   User input: EPSG:27700 
#>   wkt:
#> PROJCRS["OSGB36 / British National Grid",
#>     BASEGEOGCRS["OSGB36",
#>         DATUM["Ordnance Survey of Great Britain 1936",
#>             ELLIPSOID["Airy 1830",6377563.396,299.3249646,
#>                 LENGTHUNIT["metre",1]]],
#> ...

Les composants notables de cette description du CRS incluent le code EPSG (EPSG : 27700) et la chaîne de caractères détaillée wkt (dont seules les 5 premières lignes sont montrées).²⁸ Le fait que les unités du CRS, décrites dans le champ LENGTHUNIT, soient des mètres (plutôt que des degrés) nous indique qu’il s’agit d’un CRS projeté : st_is_longlat(london_proj) renvoie maintenant FALSE et les opérations de géométrie sur london_proj fonctionneront sans avertissement. Les opérations de création de tampon sur le london_proj utiliseront GEOS et les résultats seront retournés avec les bonnes unités de distance. La ligne de code suivante crée un tampon autour des données projetées d’exactement 100 km :

london_buff_projected = st_buffer(london_proj, 1e5)

Les géométries des trois objets london_buff* qui ont un CRS spécifié créé ci-dessus (london_buff_s2, london_buff_lonlat et london_buff_projected) créés dans les extraits de code précédents sont illustrées dans la Figure ??.

#> 
#> Attachement du package : 'tmap'
#> L'objet suivant est masqué depuis 'package:datasets':
#> 
#>     rivers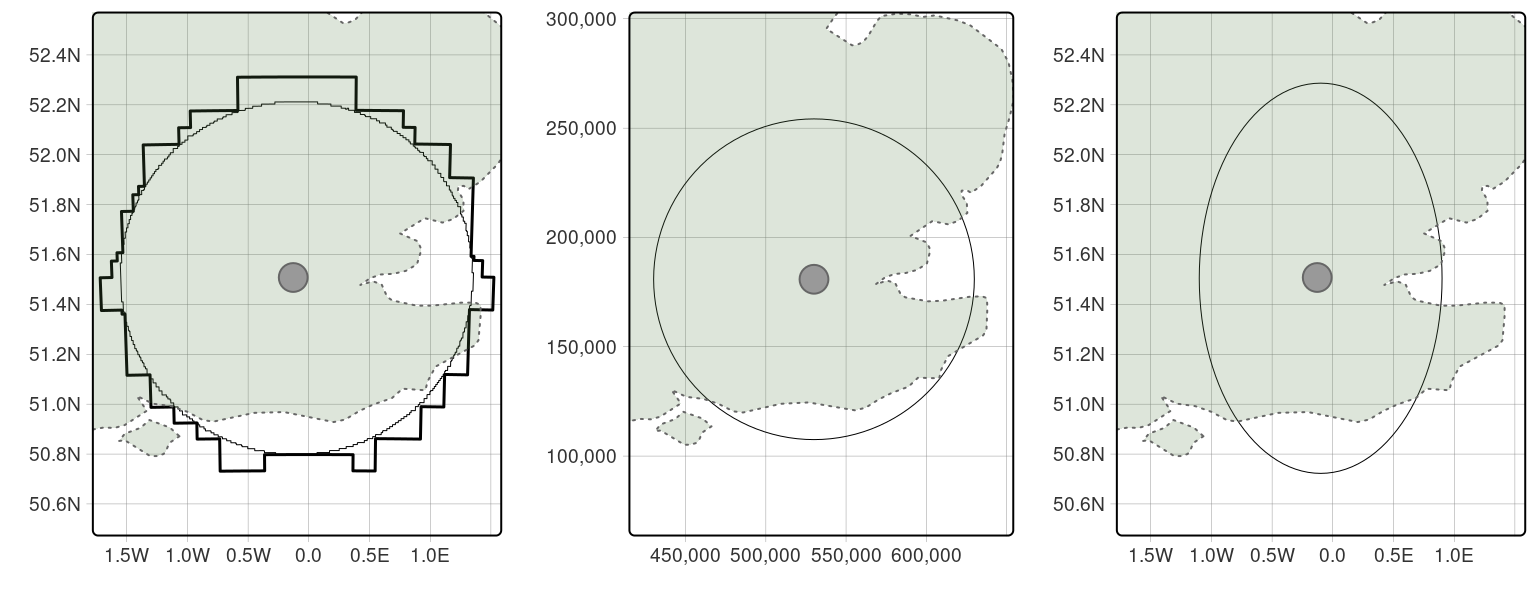

FIGURE 7.2: Tampons autour de Londres montrant les résultats créés avec le moteur de géométrie sphérique S2 sur des données long/lat (à gauche), des données projetées (au milieu) et des données long/lat sans utiliser la géométrie sphérique (à droite). Le graphique de gauche illustre le résultat des tampons sur des données non projetées avec sf, qui appelle le moteur de géométrie sphérique S2 de Google par défaut avec des cellules maximales fixées à 1000 (ligne fine). La ligne épaisse en ‘bloc’ illustre le résultat de la même opération avec des cellules maximales fixées à 100.

La figure 7.2 montre clairement que les tampons basés sur s2 et les CRS correctement projetés ne sont pas “écrasés”, ce qui signifie que chaque partie de la limite du tampon est bien équidistante de Londres. Les résultats générés à partir des CRS long/lat lorsque s2 n’est pas utilisé, soit parce que l’entrée ne comporte pas de CRS, soit parce que sf_use_s2() est désactivé, sont fortement déformés, avec un résultat allongé sur l’axe nord-sud, ce qui met en évidence les dangers de l’utilisation d’algorithmes qui supposent des données projetées sur les entrées long/lat (comme le fait GEOS). Les résultats générés à l’aide de S2 sont toutefois également faussés, mais de façon moins spectaculaire. Les deux bordures des tampons dans la Figure 7.2 (gauche) sont irrégulières, ce n’est cependant apparent ou pertinent que pour la limite épaisse représentant un tampon créé avec l’argument s2 max_cells fixé à 100. La leçon à tirer est que les résultats obtenus à partir de données long/lat via S2 seront différents des résultats obtenus en utilisant des données projetées. La différence entre les tampons dérivés de S2 et les tampons dérivés de GEOS sur des données projetées diminue lorsque la valeur de max_cells augmente : la ‘bonne’ valeur pour cet argument peut dépendre de nombreux facteurs et la valeur par défaut 1000 est une valeur raisonnable. Choisir max_cellsdépend d’un compromis entre la vitesse de calcul et la résolution des résultats. Dans les situations où les limites courbes sont avantageuses, la transformation en un CRS projeté avant la production du tampon (ou l’exécution d’autres opérations géométriques) peut être appropriée.

L’importance des CRS (principalement qu’ils soient projetés ou géographiques) et les impacts du paramètre par défaut de sf d’utiliser S2 pour les tampons sur les données long/lat ont été explicités dans l’exemple ci-dessus. Les sections suivantes vont plus en profondeur, explorant quel CRS utiliser lorsque des CRS projetés sont nécessaires et les détails de la reprojection des objets vectoriels et des rasters.

7.5 Quand reprojeter ?

La section précédente a montré comment définir manuellement le CRS, avec st_set_crs(london, "EPSG:4326"). Dans les applications réelles, cependant, les CRS sont généralement définis automatiquement lorsque les données sont lues. Dans de nombreux projets, la principale tâche liée aux CRS consiste à transformer les objets, d’un CRS à un autre. Mais quand les données doivent-elles être transformées ? Et dans quel CRS ? Il n’existe pas de réponses parfaites à ces questions et le choix d’un CRS implique toujours des compromis (Maling 1992). Cependant, certains principes généraux présentés dans cette section peuvent vous aider à prendre une décision.

Tout d’abord, il convient de se demander quand transformer. Dans certains cas, la transformation en un CRS projeté est essentielle, notamment lors de l’utilisation de fonctions géométriques telles que st_buffer(), comme l’a montré la figure 7.2. À l’inverse, la publication de données en ligne avec le package leaflet peut nécessiter un CRS géographique. Un autre cas est celui où deux objets avec des CRS différents doivent être comparés ou combinés, comme on peut le voir lorsque l’on essaie de trouver la distance entre deux objets avec des CRS différents :

st_distance(london_geo, london_proj)
# > Error: st_crs(x) == st_crs(y) is not TRUE

Pour rendre les objets london et london_proj géographiquement comparables, l’un d’entre eux doit être transformé dans le CRS de l’autre. Mais quel CRS utiliser ? La réponse dépend du contexte : de nombreux projets, notamment ceux qui impliquent une cartographie web, nécessitent des sorties en EPSG:4326, auquel cas il convient de transformer l’objet projeté. En revanche, si le projet nécessite des opérations de géométrie planaire plutôt qu’un moteur d’opérations de géométrie sphérique (par exemple pour créer des tampons aux bords lisses), il peut être intéressant de transformer les données avec un CRS géographique en un objet équivalent avec un CRS projeté, tel que le British National Grid (EPSG:27700). C’est le sujet de la section 7.7.

7.6 Quel CRS utiliser ?

La question de savoir quel CRS est délicate, et il y a rarement une “bonne” réponse : “Il n’existe pas de projections polyvalentes, toutes impliquent une distorsion lorsqu’elles sont éloignées du centre du cadre spécifié” (Bivand, Pebesma, and Gómez-Rubio 2013). De plus, vous ne devez pas vous attacher à une seule projection pour toutes les tâches. Il est possible d’utiliser une projection pour une partie de l’analyse, une autre projection pour une autre partie, et même une autre pour la visualisation. Essayez toujours de choisir le CRS qui sert le mieux votre objectif.

Lors du choix d’un de CRS géographique, celui ci se porte souvent [WGS84] (https://en.wikipedia.org/wiki/World_Geodetic_System#A_new_World_Geodetic_System:_WGS_84). Il est utilisé non seulement pour la cartographie Web, mais aussi parce que les jeux de données GPS et des milliers de jeux de données rasters et vectorielles sont fournis par défaut dans celui ci. WGS84 est le CRS le plus répandu dans le monde, il est donc utile de connaître son code EPSG : 4326. Ce “chiffre magique” peut être utilisé pour convertir des objets avec des CRS projetés inhabituels en quelque chose de largement compréhensible.

Qu’en est-il lorsqu’un CRS projeté est nécessaire ? Dans certains cas, ce n’est pas quelque chose que nous sommes libres de décider : ” souvent le choix de la projection est fait par une agence publique de cartographie ” (Bivand, Pebesma, and Gómez-Rubio 2013). Cela signifie que lorsque l’on travaille avec des sources de données locales, il est probablement préférable de travailler avec le CRS dans lequel les données ont été fournies, afin de garantir la compatibilité, même si le CRS officiel n’est pas le plus précis. L’exemple de Londres était simple car (a) le British National Grid (avec son code EPSG 27700 associé) est bien connu et (b) le jeu de données original (london) avait déjà ce CRS.

Un standard couramment utilisé est la projection universelle transverse de Mercator (UTM), un ensemble de CRS qui divise la Terre en 60 fuseaux longitudinaux et 20 segments latitudinaux. La projection transversale de Mercator utilisée par les CRS UTM est conforme mais déforme les zones et les distances avec une sévérité croissante en fonction de la distance par rapport au centre de la zone UTM. La documentation du logiciel SIG Manifold suggère donc de limiter l’étendue longitudinale des projets utilisant les zones UTM à 6 degrés du méridien central (source : manifold.net). Par conséquent, nous recommandons d’utiliser l’UTM uniquement lorsque votre objectif est de préserver les angles pour une zone relativement petite !

Presque tous les endroits de la Terre ont un code UTM, tel que “60H” qui fait référence au nord de la Nouvelle-Zélande où R a été inventé. Les codes UTM EPSG vont séquentiellement de 32601 à 32660 pour les lieux de l’hémisphère nord et de 32701 à 32760 pour les lieux de l’hémisphère sud.

Pour montrer comment le système fonctionne, créons une fonction, lonlat2UTM() pour calculer le code EPSG associé à n’importe quel point de la planète comme suit :

lonlat2UTM = function(lonlat) {
  utm = (floor((lonlat[1] + 180) / 6) %% 60) + 1
  if(lonlat[2] > 0) {
    utm + 32600
  } else{
    utm + 32700
  }
}

La commande suivante utilise cette fonction pour identifier la zone UTM et le code EPSG associé pour Auckland et Londres :

lonlat2UTM(c(174.7, -36.9))
#> [1] 32760
lonlat2UTM(st_coordinates(london))
#> [1] 32630

Actuellement, nous disposons également d’outils nous aidant à sélectionner un CRS approprié, comme le paquet crssuggest. La fonction principale de ce paquet, suggest_crs(), prend un objet spatial avec un CRS géographique et renvoie une liste de CRS projetés possibles qui pourraient être utilisés pour la zone donnée.^ [Ce paquet permet également de déterminer le véritable CRS des données sans aucune information sur le CRS]. Un autre outil utile est une page Web https://jjimenezshaw.github.io/crs-explorer/ qui répertorie les CRS en fonction du lieu et du type sélectionnés. Remarque importante : bien que ces outils soient utiles dans de nombreuses situations, vous devez connaître les propriétés du CRS recommandé avant de l’appliquer.

Dans les cas où un CRS approprié n’est pas immédiatement clair, le choix du CRS doit dépendre des propriétés qu’il est le plus important de préserver dans les cartes et analyses ultérieures. Tous les CRS sont soit à surface égale, soit équidistants, soit conformes (les formes restant inchangées), soit une combinaison de compromis de ceux-ci (section ??). Des CRS personnalisés avec des paramètres locaux peuvent être créés pour une région d’intérêt et plusieurs CRS peuvent être utilisés dans des projets quand aucun CRS unique ne convient à toutes les tâches. Les “calculs géodésiques” peuvent constituer une solution de repli si aucun CRS n’est approprié (voir proj.org/geodesic.html). Quel que soit le CRS utilisé, les résultats peuvent ne pas être précis pour des géométries couvrant des centaines de kilomètres.

Si vous décidez d’opter pour un SIR personnalisé, nous vous recommandons les éléments suivants:²⁹

• Une projection Lambert azimutale d’aire égale (LAEA) pour une projection locale personnalisée (définir la latitude et la longitude d’origine au centre de la zone d’étude), qui représente une projection de surface égale en tous lieux mais déforme les formes au-delà de milliers de kilomètres.
• Projections à équidistance azimutale (AEQD) pour des distances en ligne droite particulièrement précises entre un point et le point central de la projection locale.
• Projections coniques conformes de Lambert (LCC) pour des régions couvrant des milliers de kilomètres, avec le cône défini de manière à conserver des propriétés de distance et de surface raisonnables entre les lignes sécantes.
• Projections stéréographiques (STERE) pour les régions polaires, mais en veillant à ne pas se baser sur des calculs de surface et de distance à des milliers de kilomètres du centre.

Une approche possible pour sélectionner automatiquement un CRS projeté spécifique à un jeu de données local consiste à créer une projection azimutale équidistante (AEQD) pour le point central de la zone d’étude. Cela implique la création d’un CRS personnalisé (sans code EPSG) avec des unités en mètres basées sur le point central d’un jeu de données. Notez que cette approche doit être utilisée avec prudence : aucun autre jeu de données ne sera compatible avec le CRS personnalisé créé et les résultats peuvent ne pas être précis lorsqu’ils sont utilisés sur des jeux de données étendus couvrant des centaines de kilomètres.

Les principes décrits dans cette section s’appliquent aussi bien aux ensembles de données vectorielles qu’aux ensembles de données rasters. Certaines caractéristiques de la transformation du CRS sont toutefois propres à chaque modèle de données géographiques. Nous couvrirons les particularités de la transformation des données vectorielles dans la section 7.7 et celles de la transformation pour des rasters dans la section 7.8. Enfin, la dernière section montre comment créer des projections cartographiques personnalisées (Section 7.9).

7.7 Reprojection de géométries vectorielles

Le chapitre 2 a montré comment les géométries vectorielles sont constituées de points, et comment les points constituent la base d’objets plus complexes tels que les lignes et les polygones. Reprojeter des vecteurs consiste donc à transformer les coordonnées de ces points, qui forment les sommets des lignes et des polygones.

La section 7.5 contient un exemple dans lequel au moins un objet sf doit être transformé en un objet équivalent avec un CRS différent pour calculer la distance entre deux objets.

london2 = st_transform(london_geo, "EPSG:27700")

Maintenant qu’une version transformée de london a été créée, en utilisant la fonction sf st_transform(), la distance entre les deux représentations de Londres peut être obtenue.³⁰ La différence de localisation entre les deux points n’est pas due à des imperfections dans l’opération de transformation (qui est en fait très précise) mais à la faible précision des coordonnées créées manuellement qui ont permis de créer london et london_proj. Il est également surprenant que le résultat soit fourni dans une matrice avec des unités en mètres. C’est parce que st_distance() peut fournir des distances entre de nombreuses caractéristiques et parce que le CRS a des unités de mètres. Utilisez as.numeric() pour convertir le résultat en un nombre sans unité. ]

st_distance(london2, london_proj)
#> Units: [m]
#>      [,1]
#> [1,] 2016

Les fonctions d’interrogation et de reprojection des CRS sont présentées ci-dessous en référence à cycle_hire_osm, un objet sf de spData qui représente les “stations d’accueil” où l’on peut louer des vélos à Londres. Les CRS des objets sf peuvent être interrogés — et comme nous l’avons appris dans la section 7.1 définis — avec la fonction st_crs(). La sortie est imprimée sous forme de plusieurs lignes de texte contenant des informations sur le système de coordonnées :

st_crs(cycle_hire_osm)
#> Coordinate Reference System:
#>   User input: EPSG:4326 
#>   wkt:
#> GEOGCS["WGS 84",
#>     DATUM["WGS_1984",
#>         SPHEROID["WGS 84",6378137,298.257223563,
#>             AUTHORITY["EPSG","7030"]],
#>         AUTHORITY["EPSG","6326"]],
#>     PRIMEM["Greenwich",0,
#>         AUTHORITY["EPSG","8901"]],
#>     UNIT["degree",0.0174532925199433,
#>         AUTHORITY["EPSG","9122"]],
#>     AUTHORITY["EPSG","4326"]]

Comme nous l’avons vu dans la section 7.3, les principaux composants du CRS, User input et wkt, sont imprimés comme une seule entité, la sortie de st_crs() est en fait une liste nommée de la classe crs avec deux éléments, des chaînes de caractères uniques nommées input et wkt, comme le montre la sortie du morceau de code suivant :

crs_lnd = st_crs(london_geo)
class(crs_lnd)
#> [1] "crs"
names(crs_lnd)
#> [1] "input" "wkt"

Des éléments supplémentaires peuvent être récupérés avec l’opérateur $, notamment Name, proj4string et epsg (voir ?st_crs et le tutoriel CRS et transformation sur le site web de GDAL pour plus de détails) :

crs_lnd$Name
#> [1] "WGS 84"
crs_lnd$proj4string
#> [1] "+proj=longlat +datum=WGS84 +no_defs"
crs_lnd$epsg
#> [1] 4326

Comme mentionné dans la section 7.2, la représentation WKT, stockée dans l’élément $wkt de l’objet crs_lnd est la source ultime de vérité. Cela signifie que les sorties de la séquence de code précédente sont des requêtes provenant de la représentation wkt fournie par PROJ, plutôt que des attributs inhérents à l’objet et à son CRS.

Les deux éléments wkt et User Input du CRS sont modifiés lorsque le CRS de l’objet est transformé. Dans le morceau de code ci-dessous, nous créons une nouvelle version de cycle_hire_osm avec un CRS projeté (seules les 4 premières lignes de la sortie CRS sont montrées par souci de concision) :

cycle_hire_osm_projected = st_transform(cycle_hire_osm, "EPSG:27700")
st_crs(cycle_hire_osm_projected)
#> Coordinate Reference System:
#>   User input: EPSG:27700 
#>   wkt:
#> PROJCRS["OSGB36 / British National Grid",
#> ...

L’objet résultant a un nouveau CRS avec un code EPSG 27700. Mais comment trouver plus de détails sur ce code EPSG, ou sur n’importe quel code ? L’une des possibilités est de le rechercher en ligne,

crs_lnd_new = st_crs("EPSG:27700")
crs_lnd_new$Name
#> [1] "OSGB36 / British National Grid"
crs_lnd_new$proj4string
#> [1] "+proj=tmerc +lat_0=49 +lon_0=-2 +k=0.9996012717 +x_0=400000 +y_0=-100000 +ellps=airy +units=m +no_defs"
crs_lnd_new$epsg
#> [1] 27700

Le résultat montre que le code EPSG 27700 représente le British National Grid, un résultat qui aurait pu être trouvé en recherchant en ligne les éléments suivants “EPSG 27700”.

L’impression d’un objet spatial dans la console renvoie automatiquement ses coordonnées dans un système de référence. Pour y accéder et le modifier explicitement, utilisez la fonction st_crs, par exemple, st_crs(cycle_hire_osm).

7.8 Reprojection de rasters

Les concepts de projection décrits dans la section précédente s’appliquent également aux rasters. Cependant, il existe des différences importantes dans la reprojection des vecteurs et des rasters : La transformation d’un objet vectoriel implique la modification des coordonnées de chaque sommet, mais cela ne s’applique pas aux rasters. Les rasters sont composées de cellules rectangulaires de même taille (exprimées par des unités cartographiques, comme les degrés ou les mètres), il est donc généralement impossible de transformer les coordonnées des pixels séparément. La reprojection de rasters implique la création d’un nouvel objet raster, souvent avec un nombre de colonnes et de lignes différent de celui de l’original. Les attributs doivent ensuite être réestimés, ce qui permet de “remplir” les nouveaux pixels avec les valeurs appropriées. En d’autres termes, la reprojection matricielle peut être considérée comme deux opérations spatiales distinctes : une reprojection vectorielle de l’étendue matricielle vers un autre CRS (section 7.7), et le calcul de nouvelles valeurs de pixels par rééchantillonnage (section ??). Ainsi, dans la plupart des cas où des données rasters et vectorielles sont utilisées, il est préférable d’éviter de reprojeter des données rasters et de reprojeter des vecteurs à la place.

La reprojection des rasters est également appelée “déformation” (warping). En outre, il existe une deuxième opération similaire appelée “transformation”. Au lieu de rééchantillonner toutes les valeurs, elle laisse toutes les valeurs intactes mais recalcule de nouvelles coordonnées pour chaque cellule du raster, modifiant ainsi uniquement la géométrie de la grille. Par exemple, elle peut convertir la grille d’entrée (une grille régulière) en une grille curviligne. L’opération de transformation peut être effectuée dans R en utilisant [le paquet stars] (https://r-spatial.github.io/stars/articles/stars5.html).

Le processus de reprojection matricielle est effectué avec project() du paquetage terra. Comme la fonction st_transform() démontrée dans la section précédente, project() prend un objet géographique (un jeu de données raster dans ce cas) et une représentation CRS comme second argument. Le second argument peut aussi être un raster existant avec un CRS différent.

Examinons deux exemples de transformation de raster : l’un sur des données catégorielles et un autre sur des données continues. Les données d’occupation du sol sont généralement représentées par des cartes catégorielles. Le fichier nlcd.tif fournit des informations pour une petite zone de l’Utah, aux Etats-Unis, obtenues à partir de National Land Cover Database 2011 dans le NAD83 / UTM zone 12N CRS, comme le montre la sortie du code ci-dessous (seulement la première ligne de la sortie est affichée) :

cat_raster = rast(system.file("raster/nlcd.tif", package = "spDataLarge"))
crs(cat_raster)
#> PROJCRS["NAD83 / UTM zone 12N",
#> ...

Dans cette région, 8 classes d’occupation du sol ont été distinguées (une liste complète des classes d’occupation du sol de NLCD2011 peut être consultée à l’adresse suivante mrlc.gov):

unique(cat_raster)
#>       levels
#> 1      Water
#> 2  Developed
#> 3     Barren
#> 4     Forest
#> 5  Shrubland
#> 6 Herbaceous
#> 7 Cultivated
#> 8   Wetlands

Lors de la reprojection de rasters avec des valeurs de type catégorielles, les valeurs estimées doivent être les mêmes que celles de l’original. doivent être les mêmes que celles de l’original. Cela peut être fait en utilisant la méthode du plus proche voisin (near), qui fixe chaque nouvelle valeur de cellule à la valeur de la cellule la plus proche (via son centre) du raster d’entrée. Un exemple est la reprojection de cat_raster en WGS84, un CRS géographique bien adapté à la cartographie web. La première étape est d’obtenir la définition PROJ de ce CRS, ce qui peut être fait, par exemple en utilisant la page web http://spatialreference.org. La dernière étape consiste à reprojeter le raster avec la fonction project() qui, dans le cas de données catégorielles, utilise la méthode du plus proche voisin (near) :

cat_raster_wgs84 = project(cat_raster, "EPSG:4326", method = "near")

De nombreuses propriétés du nouvel objet diffèrent de l’ancien, notamment le nombre de colonnes et de lignes (et donc le nombre de cellules), la résolution (transformée de mètres en degrés) et l’étendue, comme l’illustre le tableau 7.1 (notez que le nombre de catégories passe de 8 à 9 en raison de l’ajout des valeurs NA, et non parce qu’une nouvelle catégorie a été créée — les classes d’occupation du sol sont préservées).

TABLE 7.1: Attributs présent dans l’original (‘cat_raster’) et reprojecté (‘cat_raster_wgs84’) pour des jeux de données categoriels.

CRS	nrow	ncol	ncell	resolution	unique_categories
NAD83	1359	1073	1458207	31.5275	8
WGS84	1246	1244	1550024	0.0003	9

La reprojection de rasters avec des valeurs numérique (avec des valeurs décimales ou dans ce cas entières) suit une procédure presque identique. Ceci est démontré ci-dessous avec srtm.tif dans spDataLarge de la Shuttle Radar Topography Mission (SRTM), qui représente la hauteur en mètres au-dessus du niveau de la mer (élévation) avec le WGS84 CRS :

con_raster = rast(system.file("raster/srtm.tif", package = "spDataLarge"))
crs(con_raster)
#> [1] "GEOGCRS[\"WGS 84\",\n    DATUM[\"World Geodetic System 1984\",\n        ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n            LENGTHUNIT[\"metre\",1]]],\n    PRIMEM[\"Greenwich\",0,\n        ANGLEUNIT[\"degree\",0.0174532925199433]],\n    CS[ellipsoidal,2],\n        AXIS[\"geodetic latitude (Lat)\",north,\n            ORDER[1],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n        AXIS[\"geodetic longitude (Lon)\",east,\n            ORDER[2],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n    ID[\"EPSG\",4326]]"

Nous allons reprojeter ce jeu de données dans un CRS projeté, mais cette fois ci avec une autre méthode que celle des plus proche voisins qui est appropriée pour les données catégorielles. Nous utiliserons plutôt la méthode bilinéaire qui calcule la valeur de la cellule de sortie sur la base des quatre cellules les plus proches dans le raster d’origine.³¹ Les valeurs du jeu de données projeté sont la moyenne pondérée par la distance des valeurs de ces quatre cellules : plus la cellule d’entrée est proche du centre de la cellule de sortie, plus son poids est élevé. Les commandes suivantes créent une chaîne de caractères représentant la zone WGS 84 / UTM 12N, et reprojettent le raster dans ce CRS, en utilisant la méthode bilinéaire :

con_raster_ea = project(con_raster, "EPSG:32612", method = "bilinear")
crs(con_raster_ea)
#> [1] "PROJCRS[\"WGS 84 / UTM zone 12N\",\n    BASEGEOGCRS[\"WGS 84\",\n        ENSEMBLE[\"World Geodetic System 1984 ensemble\",\n            MEMBER[\"World Geodetic System 1984 (Transit)\"],\n            MEMBER[\"World Geodetic System 1984 (G730)\"],\n            MEMBER[\"World Geodetic System 1984 (G873)\"],\n            MEMBER[\"World Geodetic System 1984 (G1150)\"],\n            MEMBER[\"World Geodetic System 1984 (G1674)\"],\n            MEMBER[\"World Geodetic System 1984 (G1762)\"],\n            MEMBER[\"World Geodetic System 1984 (G2139)\"],\n            ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n                LENGTHUNIT[\"metre\",1]],\n            ENSEMBLEACCURACY[2.0]],\n        PRIMEM[\"Greenwich\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n        ID[\"EPSG\",4326]],\n    CONVERSION[\"UTM zone 12N\",\n        METHOD[\"Transverse Mercator\",\n            ID[\"EPSG\",9807]],\n        PARAMETER[\"Latitude of natural origin\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8801]],\n        PARAMETER[\"Longitude of natural origin\",-111,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8802]],\n        PARAMETER[\"Scale factor at natural origin\",0.9996,\n            SCALEUNIT[\"unity\",1],\n            ID[\"EPSG\",8805]],\n        PARAMETER[\"False easting\",500000,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8806]],\n        PARAMETER[\"False northing\",0,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8807]]],\n    CS[Cartesian,2],\n        AXIS[\"(E)\",east,\n            ORDER[1],\n            LENGTHUNIT[\"metre\",1]],\n        AXIS[\"(N)\",north,\n            ORDER[2],\n            LENGTHUNIT[\"metre\",1]],\n    USAGE[\n        SCOPE[\"Engineering survey, topographic mapping.\"],\n        AREA[\"Between 114°W and 108°W, northern hemisphere between equator and 84°N, onshore and offshore. Canada - Alberta; Northwest Territories (NWT); Nunavut; Saskatchewan. Mexico. United States (USA).\"],\n        BBOX[0,-114,84,-108]],\n    ID[\"EPSG\",32612]]"

La reprojection raster sur les variables numériques entraîne également des modifications des valeurs et des propriétés spatiales, telles que le nombre de cellules, la résolution et l’étendue. Ces changements sont illustrés dans le tableau 7.2³²:

TABLE 7.2: Attributs présent dans l’original (‘con_raster’) et reprojeté (‘con_raster_ea’) pour un raster avec des valeurs continues.

CRS	nrow	ncol	ncell	resolution	mean
WGS84	457	465	212505	0.0008	1843
UTM zone 12N	515	422	217330	83.5334	1842

Bien entendu, les limites des projections terrestres 2D s´appliquent aussi bien aux données vectorielles qu´aux données rasters. Au mieux, nous pouvons respecter deux propriétés spatiales sur trois (distance, surface, direction). Par conséquent, c´est la tâche à accomplir qui détermine la projection à choisir. Par exemple, si nous nous intéressons à une densité (points par cellule de grille ou habitants par cellule de grille), nous devons utiliser une projection de surface égale (voir également le chapitre ??).

7.9 Projections cartographiques personnalisées

Les CRSs définis par les identifiants AUTHORITY:CODE tels que EPSG:4326 sont bien adaptés à de nombreuses applications. Cependant, il est souhaitable d’utiliser d’autres projections ou de créer des CRS personnalisés dans certains cas. La section 7.6 a mentionné les raisons d’utiliser des CRS personnalisés et a fourni plusieurs approches possibles. Nous montrons ici comment appliquer ces idées dans R.

L’une d’elles consiste à prendre une définition WKT existante d’un CRS, à modifier certains de ses éléments, puis à utiliser la nouvelle définition pour la reprojection. Ceci peut être fait pour les vecteurs spatiaux avec st_crs()$wkt et st_transform(), et pour les rasters avec crs() et project(), comme le montre l’exemple suivant qui transforme l’objet zion en un CRS azimutal équidistant (AEQD) personnalisé.

zion = read_sf(system.file("vector/zion.gpkg", package = "spDataLarge"))

L’utilisation d’un CRS AEQD personnalisé nécessite de connaître les coordonnées du point central d’un ensemble de données en degrés (CRS géographique). Dans notre cas, cette information peut être extraite en calculant un centroïde de la zone sion et en le transformant en WGS84.

zion_centr = st_centroid(zion)
zion_centr_wgs84 = st_transform(zion_centr, "EPSG:4326")
st_as_text(st_geometry(zion_centr_wgs84))
#> [1] "POINT (-113 37.3)"

Ensuite, nous pouvons utiliser les nouvelles valeurs obtenues pour mettre à jour la définition WKT du CRS azimutal équidistant (AEQD) vue ci-dessous. Remarquez que nous avons modifié seulement deux valeurs ci-dessous – "Central_Meridian" pour la nouvelle longitude et "Latitude_Of_Origin" pour la latitude de notre centroïde.

my_wkt = 'PROJCS["Custom_AEQD",
 GEOGCS["GCS_WGS_1984",
  DATUM["WGS_1984",
   SPHEROID["WGS_1984",6378137.0,298.257223563]],
  PRIMEM["Greenwich",0.0],
  UNIT["Degree",0.0174532925199433]],
 PROJECTION["Azimuthal_Equidistant"],
 PARAMETER["Central_Meridian",-113.0263],
 PARAMETER["Latitude_Of_Origin",37.29818],
 UNIT["Meter",1.0]]'

La dernière étape de cette approche consiste à transformer notre objet original (zion) en notre nouveau SRC personnalisé (zion_aeqd).

zion_aeqd = st_transform(zion, my_wkt)

Les projections personnalisées peuvent également être réalisées de manière interactive, par exemple à l’aide de l’application web Projection Wizard (Šavrič, Jenny, and Jenny 2016). Ce site Web vous permet de sélectionner une étendue spatiale de vos données et une propriété de distorsion, et renvoie une liste de projections possibles. La liste contient également des définitions WKT des projections que vous pouvez copier et utiliser pour des reprojections. Voir Open Geospatial Consortium (2019) pour plus de détails sur la création de définitions CRS personnalisées avec des chaînes WKT.

Les chaînes PROJ peuvent également être utilisées pour créer des projections personnalisées, en acceptant les limitations inhérentes aux projections, notamment des géométries couvrant de grandes zones géographiques, mentionnées dans la section 7.2. De nombreuses projections ont été développées et peuvent être définies à l’aide de l’élément +proj= des chaînes PROJ. Des dizaines de projets sont décrits en détail rien que sur le site PROJ.

Lorsqu’il s’agit de cartographier le monde tout en préservant les relations entre surfaces, la projection de Mollweide, illustrée dans la figure 7.3, est un choix populaire et souvent judicieux (Jenny et al. 2017). Pour utiliser cette projection, nous devons la spécifier en utilisant l’élément proj-string, "+proj=moll", dans la fonction st_transform :

world_mollweide = st_transform(world, crs = "+proj=moll")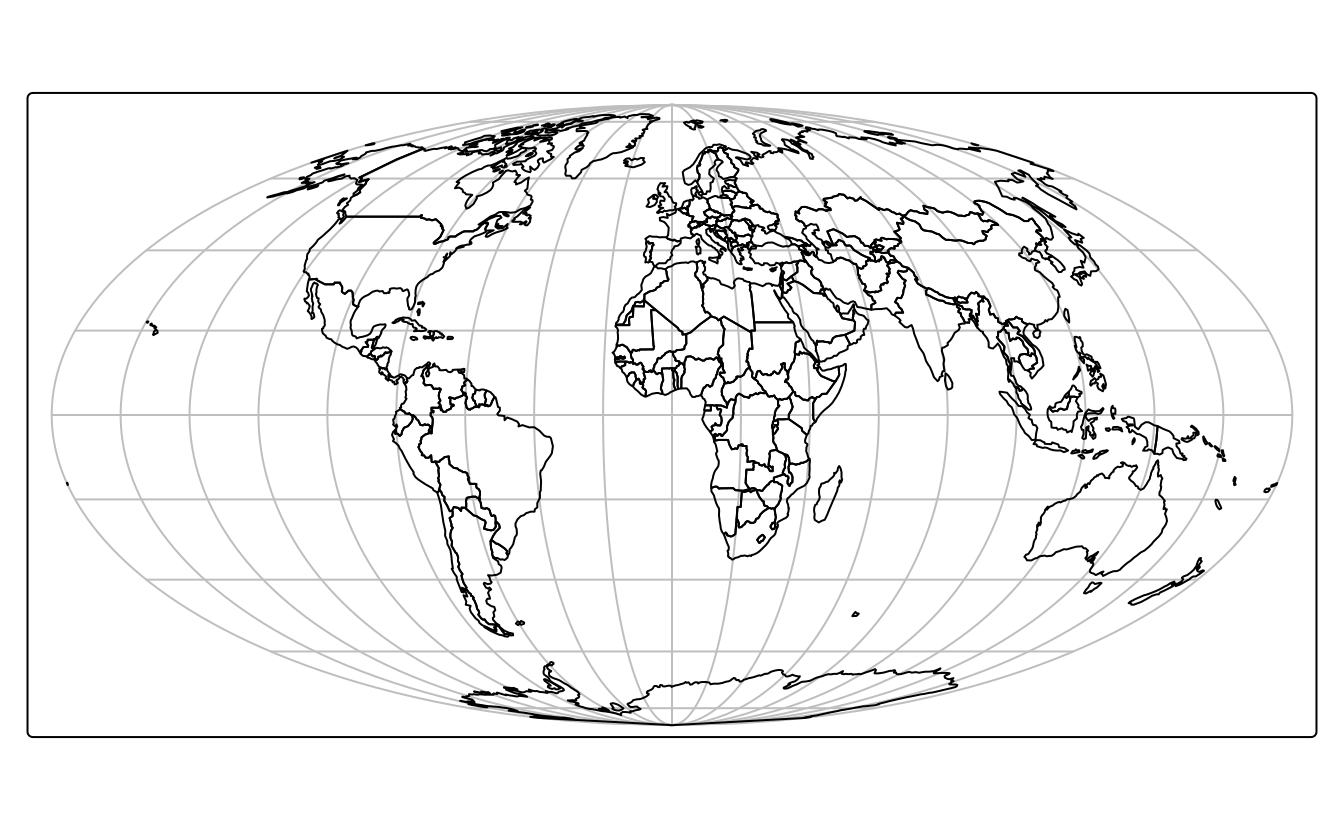

FIGURE 7.3: Représentation du monde avec la projection de Mollweide.

Il est souvent souhaitable de minimiser la distorsion pour toutes les propriétés spatiales (surface, direction, distance) lors de la cartographie du monde. L’une des projections les plus populaires permettant d’atteindre cet objectif est celle de Winkel tripel, illustrée sur la figure 7.4.³³ Le résultat a été créé avec la commande suivante :

world_wintri = st_transform(world, crs = "+proj=wintri")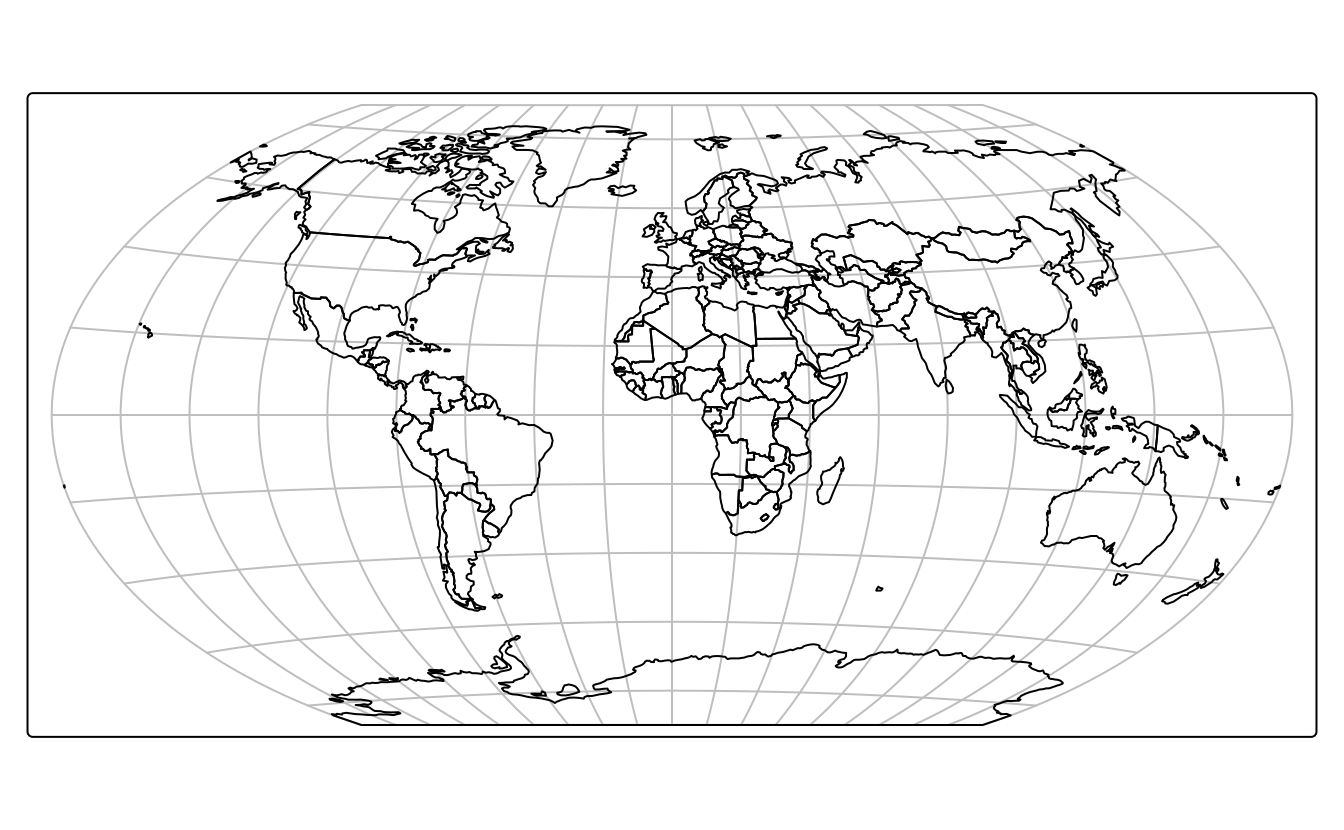

FIGURE 7.4: Repréentation du monde avec la projection Winkel tripel.

De plus, les paramètres proj-string peuvent être modifiés dans la plupart des définitions CRS, par exemple le centre de la projection peut être ajusté en utilisant les paramètres +lon_0 et +lat_0. Le code ci-dessous transforme les coordonnées en une projection de Lambert azimutale à aire égale centrée sur la longitude et la latitude de la ville de New York (Figure 7.5).

world_laea2 = st_transform(world,
                           crs = "+proj=laea +x_0=0 +y_0=0 +lon_0=-74 +lat_0=40")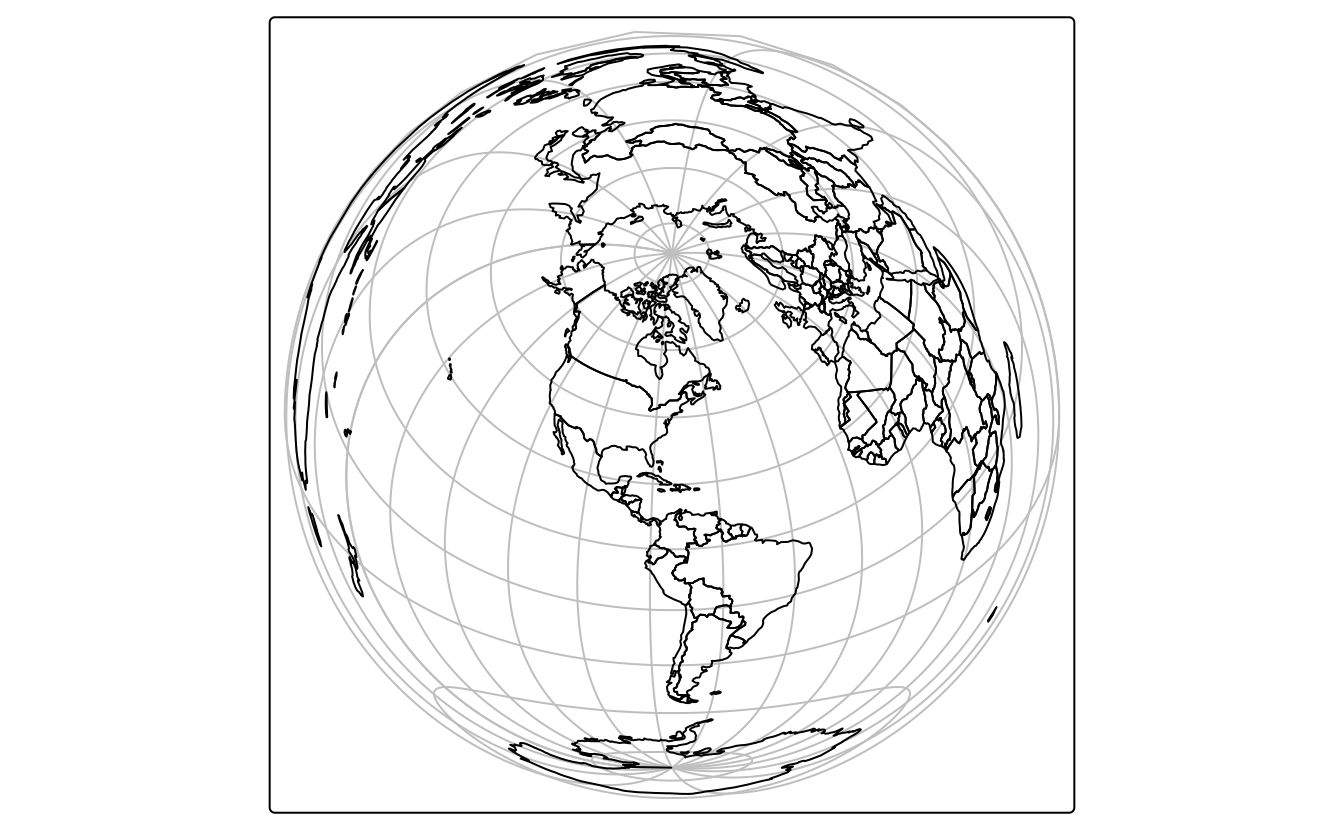

FIGURE 7.5: Projection azimutale Lambert du monde centrée sur la ville de New York

Vous trouverez de plus amples informations sur les modifications de CRS dans la documentation Using PROJ.

7.10 Exercises

E1. Créez un nouvel objet appelé nz_wgs en transformant l’objet nz avec le CRS WGS84.

• Créez un objet de la classe crs pour les deux et utilisez-le pour interroger leurs CRS respectifs.
• En se référant au rectangle de délimitation de chaque objet, quelles unités chaque CRS utilise-t-il ?
• Retirez le CRS de nz_wgs et tracez le résultat : qu’est-ce qui ne va pas avec cette carte de la Nouvelle-Zélande et pourquoi ?

E2. Transformez le jeu de données world en projection transversale de Mercator ("+proj=tmerc") et tracez le résultat. Qu’est-ce qui a changé et pourquoi ? Essayez de le retransformer en WGS 84 et tracez le nouvel objet. Pourquoi le nouvel objet est-il différent de l’objet original ?

E3. Transformez le raster de valeurs continues (con_raster) en NAD83 / zone UTM 12N en utilisant la méthode d’interpolation du plus proche voisin. Qu’est-ce qui a changé ? Comment cela influence-t-il les résultats ?

E4. Transformer le raster avec de catégories (cat_raster) en WGS 84 en utilisant la méthode d’interpolation bilinéaire. Qu’est-ce qui a changé ? Comment cela influence-t-il les résultats ?

Akima, Hiroshi, and Albrecht Gebhardt. 2016. Akima: Interpolation of Irregularly and Regularly Spaced Data. https://CRAN.R-project.org/package=akima.

Baddeley, Adrian, Ege Rubak, and Rolf Turner. 2015. Spatial Point Patterns: Methodology and Applications with R. CRC Press.

Bivand, Roger. 2000. “Using the R Statistical Data Analysis Language on GRASS 5.0 GIS Database Files.” Computers & Geosciences 26 (9): 1043–52. https://doi.org/10.1016/S0098-3004(00)00057-1.

———. 2001. “More on Spatial Data Analysis.” R News 1 (3): 13–17.

———. 2003. “Approaches to Classes for Spatial Data in R.” In Proceedings of DSC, edited by Kurt Hornik, Friedrich Leisch, and Achim Zeileis. https://www.r-project.org/nosvn/conferences/DSC-2003/Proceedings/Bivand.pdf.

———. 2016a. Rgrass7: Interface Between GRASS 7 Geographical Information System and R. https://CRAN.R-project.org/package=rgrass7.

———. 2016b. Spgrass6: Interface Between GRASS 6 and R. http://CRAN.R-project.org/package=spgrass6.

———. 2017. Spdep: Spatial Dependence: Weighting Schemes, Statistics and Models. https://CRAN.R-project.org/package=spdep.

———. 2021. “Progress in the R Ecosystem for Representing and Handling Spatial Data.” Journal of Geographical Systems 23 (4): 515–46. https://doi.org/ghnwg3.

Bivand, Roger, and Albrecht Gebhardt. 2000. “Implementing Functions for Spatial Statistical Analysis Using the Language.” Journal of Geographical Systems 2 (3): 307–17. https://doi.org/10.1007/PL00011460.

Bivand, Roger, Tim Keitt, and Barry Rowlingson. 2018. Rgdal: Bindings for the ’Geospatial’ Data Abstraction Library. https://CRAN.R-project.org/package=rgdal.

Bivand, Roger, and Nicholas Lewin-Koh. 2017. Maptools: Tools for Reading and Handling Spatial Objects. https://CRAN.R-project.org/package=maptools.

Bivand, Roger, and Markus Neteler. 2000. “Open Source Geocomputation: Using the R Data Analysis Language Integrated with GRASS GIS and PostgreSQL Data Base Systems.” In Proceedings of the 5th International Conference on GeoComputation, edited by Markus Neteler and Roger S. Bivand. http://www.geocomputation.org/2000/GC009/Gc009.htm.

Bivand, Roger, Edzer Pebesma, and Virgilio Gómez-Rubio. 2013. Applied Spatial Data Analysis with R. Vol. 747248717. Springer. https://books.google.com?id=v0eIU9ObJXgC.

Bivand, Roger, and Colin Rundel. 2018. Rgeos: Interface to Geometry Engine - Open Source (’GEOS’). https://CRAN.R-project.org/package=rgeos.

Bondaruk, Ben, Steven A. Roberts, and Colin Robertson. 2020. “Assessing the State of the Art in Discrete Global Grid Systems: OGC Criteria and Present Functionality.” Geomatica 74 (1): 9–30. https://doi.org/10.1139/geomat-2019-0015.

Brenning, Alexander. 2012. ArcGIS Geoprocessing in R via Python. https://CRAN.R-project.org/package=RPyGeo.

Brenning, Alexander, Donovan Bangs, and Marc Becker. 2018. RSAGA: SAGA Geoprocessing and Terrain Analysis. https://CRAN.R-project.org/package=RSAGA.

Brzustowicz, Michael R. 2017. Data Science with Java: [Practical Methods for Scientists and Engineers]. First. Beijing Boston Farnham: O´Reilly.

Burrough, P. A., Rachael McDonnell, and Christopher D. Lloyd. 2015. Principles of Geographical Information Systems. Third. Oxford, New York: Oxford University Press.

Calenge, C. 2006. “The Package Adehabitat for the R Software: Tool for the Analysis of Space and Habitat Use by Animals.” Ecological Modelling 197: 1035. https://doi.org/10.1016/j.ecolmodel.2006.03.017.

Chambers, John M. 2016. Extending R. CRC Press. https://books.google.com?id=kxxjDAAAQBAJ.

Clementini, Eliseo, and Paolino Di Felice. 1995. “A Comparison of Methods for Representing Topological Relationships.” Information Sciences - Applications 3 (3): 149–78. https://doi.org/ddtnhx.

Cooley, David. 2020. Sfheaders: Converts Between r Objects and Simple Feature Objects. Manual. https://CRAN.R-project.org/package=sfheaders.

Coppock, J Terry, and David W Rhind. 1991. “The History of GIS.” Geographical Information Systems: Principles and Applications, Vol. 1. 1 (1): 21–43. https://www.geos.ed.ac.uk/~gisteac/ilw/generic_resources/books_and_papers/Thx1ARTICLE.pdf.

Dieck, Tammo tom. 2008. Algebraic Topology. EMS Textbooks in Mathematics. Zürich: European Mathematical Society. https://www.maths.ed.ac.uk/~v1ranick/papers/diecktop.pdf.

Douglas, David H, and Thomas K Peucker. 1973. “Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature.” Cartographica: The International Journal for Geographic Information and Geovisualization 10 (2): 112–22. https://doi.org/bjwv52.

Dunnington, Dewey. 2021. Ggspatial: Spatial Data Framework for Ggplot2. Manual. https://CRAN.R-project.org/package=ggspatial.

Eddelbuettel, Dirk, and James Joseph Balamuta. 2018. “Extending R with C++: A Brief Introduction to Rcpp.” The American Statistician 72 (1): 28–36. https://doi.org/gdg3fb.

Egenhofer, Max, and John Herring. 1990. “A Mathematical Framework for the Definition of Topological Relations.” In Proc. The Fourth International Symposium on Spatial Data Handing, 803–13.

Garrard, Chris. 2016. Geoprocessing with Python. Shelter Island, NY: Manning Publications.

Gillespie, Colin, and Robin Lovelace. 2016. Efficient R Programming: A Practical Guide to Smarter Programming. O’Reilly Media. https://csgillespie.github.io/efficientR/.

Giraud, Timothée. 2021. Mapsf: Thematic Cartography. Manual. https://CRAN.R-project.org/package=mapsf.

Grolemund, Garrett, and Hadley Wickham. 2016. R for Data Science. O’Reilly Media.

Hijmans, Robert J. 2016. Geosphere: Spherical Trigonometry. https://CRAN.R-project.org/package=geosphere.

———. 2017. Raster: Geographic Data Analysis and Modeling. https://CRAN.R-project.org/package=raster.

———. 2021. Terra: Spatial Data Analysis. Manual. https://rspatial.org/terra/.

Ince, E. S., F. Barthelmes, S. Reißland, K. Elger, C. Förste, F. Flechtner, and H. Schuh. 2019. “ICGEM – 15 Years of Successful Collection and Distribution of Global Gravitational Models, Associated Services, and Future Plans.” Earth System Science Data 11 (2): 647–74. https://doi.org/gg5tzm.

Jenny, Bernhard, Bojan Šavrič, Nicholas D Arnold, Brooke E Marston, and Charles A Preppernau. 2017. “A Guide to Selecting Map Projections for World and Hemisphere Maps.” In Choosing a Map Projection, edited by Miljenko Lapaine and Lynn Usery, 213–28. Springer.

Jr, Paulo J. Ribeiro, and Peter J. Diggle. 2016. geoR: Analysis of Geostatistical Data. https://CRAN.R-project.org/package=geoR.

Kahle, D, and Hadley Wickham. 2013. “Ggmap: Spatial Visualization with Ggplot2.” The R Journal 5: 144–61. https://doi.org/10.32614/RJ-2013-014.

Lamigueiro, Oscar Perpinan. 2018. Displaying Time Series, Spatial, and Space-Time Data with R. Second. Boca Raton: Chapman and Hall/CRC.

Liu, Jian-Guo, and Philippa J. Mason. 2009. Essential Image Processing and GIS for Remote Sensing. Chichester, West Sussex, UK, Hoboken, NJ: Wiley-Blackwell.

Livingstone, David N. 1992. The Geographical Tradition: Episodes in the History of a Contested Enterprise. Oxford, UK ; Cambridge, USA: John Wiley & Sons Ltd.

Loecher, Markus, and Karl Ropkins. 2015. “RgoogleMaps and Loa: Unleashing R Graphics Power on Map Tiles.” Journal of Statistical Software 63 (February): 1–18. https://doi.org/gfgwng.

Longley, Paul. 2015. Geographic Information Science & Systems. Fourth edition. Hoboken, NJ: Wiley.

Longley, Paul, Sue M. Brooks, Rachael McDonnell, and Bill MacMillan, eds. 1998. Geocomputation: A Primer. Chichester, Eng. ; New York: Wiley.

Majure, James J., and Albrecht Gebhardt. 2016. Sgeostat: An Object-Oriented Framework for Geostatistical Modeling in S+. https://CRAN.R-project.org/package=sgeostat.

Maling, D. H. 1992. Coordinate Systems and Map Projections. Second. Oxford ; New York: Pergamon Press.

“Map Projections.” 1993. US Geological Survey. https://doi.org/10.3133/70047422.

Morgan-Wall, Tyler. 2021. Rayshader: Create Maps and Visualize Data in 2D and 3D. Manual. https://CRAN.R-project.org/package=rayshader.

Muenchow, Jannes, Patrick Schratz, and Alexander Brenning. 2017. “RQGIS: Integrating R with QGIS for Statistical Geocomputing.” The R Journal 9 (2): 409–28. https://doi.org/gf3d48.

Neteler, Markus, and Helena Mitasova. 2008. Open Source GIS: A GRASS GIS Approach. Third. New York, NY: Springer.

Open Geospatial Consortium. 2019. “Well-Known Text Representation of Coordinate Reference Systems.” Implementation Standard 18-010r7. Geographic Information. Open Geospatial Consortium. https://docs.opengeospatial.org/is/18-010r7/18-010r7.html.

Openshaw, Stan, and Robert J. Abrahart, eds. 2000. Geocomputation. London ; New York: CRC Press.

Pebesma, Edzer. 2018. “Simple Features for R: Standardized Support for Spatial Vector Data.” The R Journal. https://doi.org/gf2ztt.

———. 2021. Stars: Spatiotemporal Arrays, Raster and Vector Data Cubes. Manual. https://CRAN.R-project.org/package=stars.

Pebesma, Edzer, and Roger Bivand. 2005. “Classes and Methods for Spatial Data in R.” R News 5 (2): 9–13. https://cran.r-project.org/doc/Rnews/Rnews_2005-2.pdf.

———. 2018. Sp: Classes and Methods for Spatial Data. https://CRAN.R-project.org/package=sp.

———. 2022. Spatial Data Science with Applications in R. https://r-spatial.org/book.

Pebesma, Edzer, and Benedikt Graeler. 2018. Gstat: Spatial and Spatio-Temporal Geostatistical Modelling, Prediction and Simulation. https://CRAN.R-project.org/package=gstat.

Pebesma, Edzer, Thomas Mailund, and James Hiebert. 2016. “Measurement Units in R.” The R Journal 8 (2): 486–94. https://doi.org/gkb5pd.

Pebesma, Edzer, Daniel Nüst, and Roger Bivand. 2012. “The R Software Environment in Reproducible Geoscientific Research.” Eos, Transactions American Geophysical Union 93 (16): 163–63. https://doi.org/gd8djc.

Pedersen, Thomas Lin, and David Robinson. 2020. Gganimate: A Grammar of Animated Graphics. Manual. https://CRAN.R-project.org/package=gganimate.

Qiu, Fang, Caiyun Zhang, and Yuhong Zhou. 2012. “The Development of an Areal Interpolation ArcGIS Extension and a Comparative Study.” GIScience & Remote Sensing 49 (5): 644–63. https://doi.org/gkb5fn.

R Core Team, D. M. Smith, and R Core Team. 2021. An Introduction to R. https://cran.r-project.org/doc/manuals/r-release/R-intro.html.

Ripley, Brian D. 2001. “Spatial Statistics in R.” R News 1 (2): 14–15.

Roussel, Jean-Romain, David Auty, Nicholas C. Coops, Piotr Tompalski, Tristan R. H. Goodbody, Andrew Sánchez Meador, Jean-François Bourdon, Florian de Boissieu, and Alexis Achim. 2020. “lidR: An r Package for Analysis of Airborne Laser Scanning (ALS) Data.” Remote Sensing of Environment 251 (December): 112061. https://doi.org/ghddxb.

Rowlingson, B. S, and P. J Diggle. 1993. “Splancs: Spatial Point Pattern Analysis Code in S-plus.” Computers & Geosciences 19 (5): 627–55. https://doi.org/dvzffd.

Rowlingson, Barry, Adrian Baddeley, Rolf Turner, and Peter Diggle. 2003. “Rasp: A Package for Spatial Statistics.” In Proceedings of the 3rd International Workshop on Distributed Statistical Computing, edited by Kurt Hornik. https://www.r-project.org/conferences/DSC-2003/Proceedings/RowlingsonEtAl.pdf.

Rowlingson, Barry, and Peter Diggle. 2017. Splancs: Spatial and Space-Time Point Pattern Analysis. https://CRAN.R-project.org/package=splancs.

Šavrič, Bojan, Bernhard Jenny, and Helen Jenny. 2016. “Projection Wizard – An Online Map Projection Selection Tool.” The Cartographic Journal 53 (2): 177–85. https://doi.org/ggsx6z.

Shen, Jingwei, Min Chen, and Xintao Liu. 2018. “Classification of Topological Relations Between Spatial Objects in Two-Dimensional Space Within the Dimensionally Extended 9-Intersection Model.” Transactions in GIS 22 (2): 514–41. https://doi.org/gnhcx9.

Sherman, Gary. 2008. Desktop GIS: Mapping the Planet with Open Source Tools. Pragmatic Bookshelf.

Spanier, Edwin Henry. 1995. Algebraic Topology. 1. corr. Springer ed. New York Berlin Barcelona Budapest: Springer.

Talbert, Richard J. A. 2014. Ancient Perspectives: Maps and Their Place in Mesopotamia, Egypt, Greece, and Rome. University of Chicago Press. https://books.google.com?id=srTbAgAAQBAJ.

Tennekes, Martijn, and Jakub Nowosad. 2022. Elegant and Informative Maps with Tmap.

The Economist. 2016. “The Autonomous Car’s Reality Check.” The Economist, 2016. https://www.economist.com/news/science-and-technology/21696925-building-highly-detailed-maps-robotic-vehicles-autonomous-cars-reality.

Tobler, Waldo R. 1979. “Smooth Pycnophylactic Interpolation for Geographical Regions.” Journal of the American Statistical Association 74 (367): 519–30. https://doi.org/ghz78f.

Tomlin, C. Dana. 1990. Geographic Information Systems and Cartographic Modeling. Englewood Cliffs, N.J: Prentice Hall.

———. 1994. “Map Algebra: One Perspective.” Landscape and Urban Planning 30 (1-2): 3–12. https://doi.org/dm2qm2.

Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with S. Fourth. New York: Springer. http://www.stats.ox.ac.uk/pub/MASS4.

Visvalingam, M., and J. D. Whyatt. 1993. “Line Generalisation by Repeated Elimination of Points.” The Cartographic Journal 30 (1): 46–51. https://doi.org/fx74gh.

Wegmann, Martin, Benjamin Leutner, and Stefan Dech, eds. 2016. Remote Sensing and GIS for Ecologists: Using Open Source Software. Data in the Wild. Exeter: Pelagic Publishing.

Wickham, Hadley. 2019. Advanced R, Second Edition. CRC Press. https://adv-r.hadley.nz/.

Wulf, Andrea. 2015. The Invention of Nature: Alexander von Humboldt’s New World. New York: Alfred A. Knopf.